06 Modeling

in Notes / Dataanalytics / Datascience

Introduction

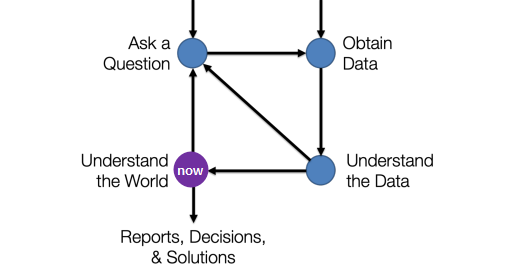
  • Understand the World: starting machine learning lifecycle

Model : idealized representation of a system

  • not exact nor correct (approximated but accurate enough)

  • Why do we build Models?
    1. To understand complex phenomena occuring in the world we live in
      • simple and interpretable physics velocity, acceleration
    2. To make accurate predictions about unseen data
      • predicting email is spam/not
      • black-box models: making extremely accurate predictions but uninterpretable model
  • Learning from DATA
    • no analytic solution (or hard to get) but have data \(\Rightarrow\) use Data!
    • no need to do everything my mathematical modeling
    Example: Recommendation Systems 
    - `20%` sales from recommendation (Amazon)
- `10%` improvement = 1 million dollar prize (Netflix)

    lifecycle

    • power of learning from data: entire process can be automated without having to look at video content or viewer taste
    • Dall-E2, ChatGPT all based on Data
    • The essence of learning from data
      1. We have data
      2. A pattern exists therin
      3. We cannot pin it down analyticall (or is challenging)

Notations

  • \(y\) : true observations (Ground Truth)
  • \(\hat{y}\) : predicted observations
  • \(\theta\) : parameter(s) of model (what we are trying to estimate)
    • not all models have parameters ex: KDE

  • \(\hat{\theta}\) : fitted/optimal parameter(s) we solve for \(\Leftarrow\) goal (Final Parameter)

  • \(tune \theta\) to minimize \(y\) and \(\hat{y}\)

Constant Model

Constant Model

: ignore any relationships between variables and predict the same number for each individual (predicting constant)

  • aka summary statistic (of data)
\[\hat{y} = \theta\]
  • GOAL: find \(\hat{\theta}\)
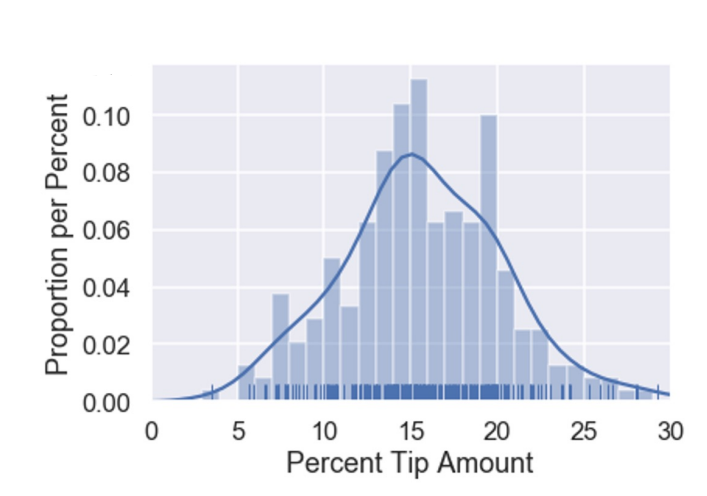
  • Case Study: Tips
    • model to predict some numerical quantity of population:
      1. percentage tip given at restaurants
      2. GPA of students and Korea University
    • Constant model: ignoring total bill price, time of day, customers’ emotion…when predicting tips lifecycle

  • Prediction vs Estimation

    Estimationtask of using data to determine model parameters
    Predictiontask of using a model to predict output (for unseen data)
    • if estimates exist for model paramters then can use model for prediction

Loss Functions

Loss

: cost of making prediction

  • metric of how good or bad our predictions are
  • if prediction \(\leftrightarrow\) actual value \(\Rightarrow\) low loss

  • if prediction \(\longleftrightarrow\) actual value \(\Rightarrow\) high loss

  • error

    for a single prediction: = actual - predicted (\(y_i - \hat{y_i}\))

    • natural choice of loss function
    • BUT this treats negative and positive predictions differently
      • value = `15`; predicting `16` should equal to predicting `14`
      • \(\Rightarrow\) 2 natural loss functions

Squared Loss

\(L_2(y, \hat{y}) = (y-\hat{y})^2\)

  • single data point in general = \((y-\hat{y})^2\)

  • constant model (since \(\hat{y}=\theta\)) = \((y_i-\theta)^2\)

  • if prediction === actual observation \(\Rightarrow\) loss = 0
    • low loss \(\Rightarrow\) Good Fit!

Absolute Loss

\(L_1(y, \hat{y}) = |y-\hat{y}|\)

  • constant model \((\hat{y}=\theta ) = [y-\theta]\)

  • if prediction === actual observation \(\Rightarrow\) loss = 0
    • low loss \(\Rightarrow\) Good Fit!
  • both loss functions have drawbacks; there are more loss functions

Emprical Risk

  • average loss across all points (not just a single point)

\(\frac{1}{n}\sum_{i=1}^n L(y_i, \hat{y_i})\)

  • tells how well model fits the given data
  • find parameter(s) minimizing the average loss
  • aka emipirical risk, objective function

MSE and MAE

MSEMean Squared Errorsquared loss\(MSE(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^n(y_i-\hat{y_i})^2\)
MAEMean Absolute Errorabsolute loss\(MAE(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^n[y_i-\hat{y_i}]\)

MSE

  • average loss typically written as a function of \(\theta\)

\(R(\theta) = \frac{1}{n}\sum_{i=1}^n(y_i-\hat{y_i})^2\) \(\rightarrow \hat{\theta} =\) argmin \(\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y_i})^2\)

  • argmin = argument that minimizes the following function
  • in constant model (\(\hat{y} = \theta\)) \(\Rightarrow\) \(R(\theta) = \frac{1}{n}\sum_{i=1}^n(y_i-\theta)^2\)
  • example: 5 observations [20, 21, 22, 29, 33]
    • loss for first point (20) \(L_2(20, \theta)=(20-\theta)^2\)
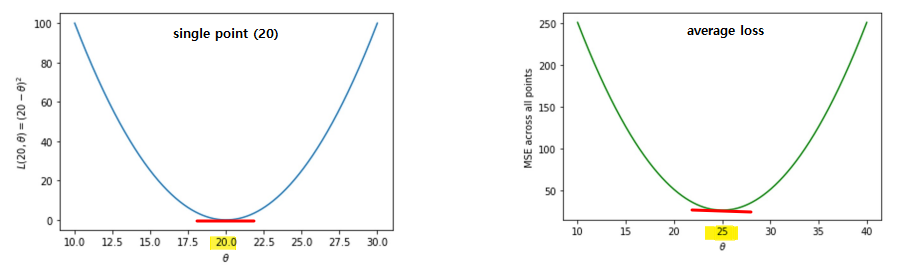
    • average loss across all observations : \(R(\theta) = \frac{1}{5}((20-\theta)^2+(21-\theta)^2+(22-\theta)^2+(29-\theta)^2+(33-\theta)^2)\) lifecycle
      • both parabola
      • loss for first observation = minimized at 20
      • average loss = minimized at 25
MSE = *mean*

of observations in constant models

  • Proof 1 : Using Calculus
    • take derivate \(\rightarrow\) set to 0 \(\rightarrow\) solve for optimizing value \(\rightarrow\) take second derivate to check convex direction (positive = upwards )
    \[R(\theta) = \frac{1}{n}\sum_{i=1}^n(y_i-\theta)^2\]
    1. take derivative
      • \(\frac{d}{d\theta}R(\theta)\) = \(\frac{1}{n}\sum_{i=1}^n\frac{d}{d\theta}(y_i-\theta)^2\)
      • = \(\frac{1}{n}\sum_{i=1}^n(-2)(y_i-\theta)\)
      • = \(\frac{-2}{n}\sum_{i=1}^n(y_i-\theta)\)
    2. set derivate equal to 0 (find minimum point)
      • 0 =\(\frac{-2}{n}\sum_{i=1}^n(y_i-\hat{y_i})\)
      • 0 =\(\sum_{i=1}^n(y_i-\theta)\)
      • 0=\(\sum_{i=1}^n(y_i)-n\theta\)
      • \(n\theta\) = \(\sum_{i=1}^n(y_i)\)
      • \(\hat{\theta}\) = \(\frac{1}{n}\sum_{i=1}^n(y_i) \Rightarrow mean\)
    3. take second derivative
      • \(\frac{d}{d\theta}R(\theta)\) = \(\frac{-2}{n}\sum_{i=1}^n(y_i-\theta)\)
      • \(\frac{d^2}{d\theta^2}R(\theta)\) = \(\frac{-2}{n}\sum_{i=1}^n(0-1)\)
      • = \(\frac{2}{n}\sum_{i=1}^n(1)\) = \(2\)
      • \(\Rightarrow\) positive at convex!
  • Proof 2 : Using Algebraic Trick
    • refresh:
    • (1) sum of deviations from mean = 0 \(\sum_{i=1}^n(y_i-\hat{y})=0\)
    • (2) definition of variance \(\sigma_y^2=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y})^2\) lifecycle
    • TBwritteninlatex later on...
    • \(R(\theta)\) = \(\sigma_y^2 + (\hat{y}-\theta)^2\)
      • both terms = postive (variance and squared can’t be negative)
      • first term does not contain \(\theta \rightarrow\) ignore
      • second term contains \(\theta \rightarrow\) can be minimized (to 0) if \(\theta = \hat{y}\)
      • \[\Rightarrow \hat{\theta} = \hat{y} = mean(y)\]

MAE

  • mean absolute error
\[R(\theta) = \frac{1}{n}\sum_{i=1}^n|y_i-\theta|\]
  • example: 5 observations [20, 21, 22, 29, 33]
    • loss for first point (20) \(L_2(20, \theta)=\mid 20-\theta \mid\)
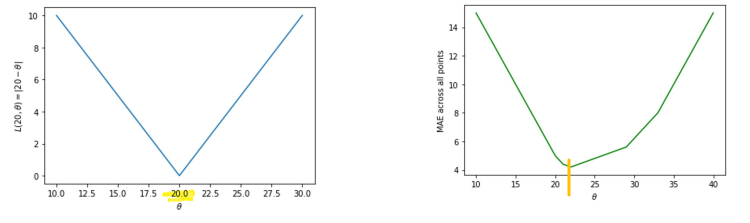
    • average loss across all observations : \(R(\theta) = \frac{1}{5}(|20-\theta|+|21-\theta|+|22-\theta|+|29-\theta|+|33-\theta|)\) lifecycle
      • both absolute value curve
      • loss for first observation = minimized at 20
      • average loss = minimized at \(\approx\) 22
    • results in piecewise linear function (seems to be jagged)
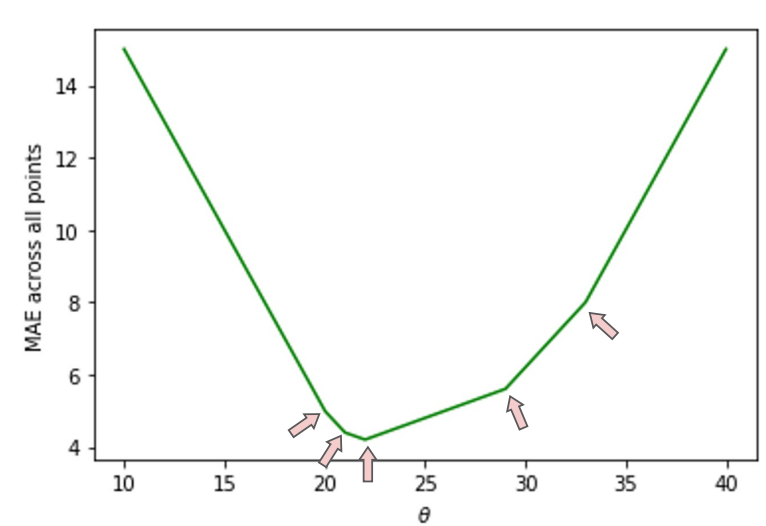
      • seemingly not \(mean\) lifecycle
      • bends (kinks) appear at observations ([20, 21, 22, 29, 33])
  • MAE minimization using Calculus
    • piecewise linear function (since it’s absolute) \(|y_i-\theta| = \begin{cases} y_i-\theta, \theta<=y_i\\ \theta-y_i, \theta>y_i \end{cases}\)

    1. take derivative

      • \(\frac{d}{d\theta}\mid y_i-\theta \mid\) = \(\begin{cases} -1, \theta<=y_i\\ 1, \theta>y_i \end{cases}\)

      • derivative of sum = sum of derivatives
      • \(\frac{d}{d\theta}R(\theta)\)=\(\frac{1}{n}\sum_{i=1}^n \frac{d}{d\theta} \mid y_i-\theta \mid\)
      • = \(\frac{1}{n}[\sum_{\theta<y_i}(-1)+\sum_{\theta>y_i}(1)]\)

    2. set derivative equal to 0 (find minimum point)

      • 0 = \(\frac{1}{n}[\sum_{\theta<y_i}(-1)+\sum_{\theta>y_i}(1)]\)
      • 0 = \(-\sum_{\theta<y_i}(1)+\sum_{\theta>y_i}(1)\)
      • \(\sum_{\theta<y_i}(1)\)=\(\sum_{\theta>y_i}(1)\) - \(\Rightarrow\) # of observations less than theta == number of observations greater than theta - \(\Rightarrow\) equal number of points on both left/right side - \(\Rightarrow \hat{\theta} = median(y)\)
  • if even number of observations:
    • ex: [20, 21, 22, 29, 33, 35] \(\rightarrow\) no unique solution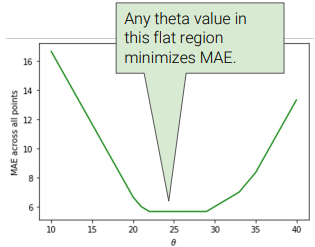 lifecycle
    • any value in range [22,29] minimizes MAE
    • usually, mean of those medians are used (25.5)

MSE vs MAE

  • loss surface

    plot of the loss encountered for each possible value of \(\theta\)

    • ex: 2 parameters for model \(\rightarrow\) plot = 3-D
  • MSE vs MAE
Mean Squared ErrorMean Absolute Error
Sample MeanSample Median
very smooth (easy to minimize)not as smooth (kinks=not differentiable), harder to minimize
very sensitive to outliersrobust to outliers
  • not clear if one is better than the other (we get to choose!)

Summary

  1. Choose a model
    • constant model (in this case) with single parameter
  2. Choose a loss function (\(L_2, L_1\))
  3. Fit the model by minimizing average loss
    • choose optimal parameters to minimize average loss
    • aka fitting model to the data