09 Logistic Regression

04 May 2023 in Notes / Dataanalytics / Datascience

Logistic Regression I
Logistic Regression II

Logistic Regression I

Machine Learning Taxonomy

Supervised Learning
(Labeled Data)
- Regression : Quantitative Response still mostly used for classification...
- Classification : Categorical Response
Unsupervised Learning (Unlabeled Data)
- Dimensionality Reduction
- Clustering
Reinforcement Learning (Reward) Alpha Go
- Learning Paradigm: use of ??data to uncover an underlying process

Supervised Learning

most studied and utilized
training data contains explicit examples of what the ??output should be for given inputs \(\rightarrow Supervised\)
- correct label exists
Typical Supervised Learning Procedure

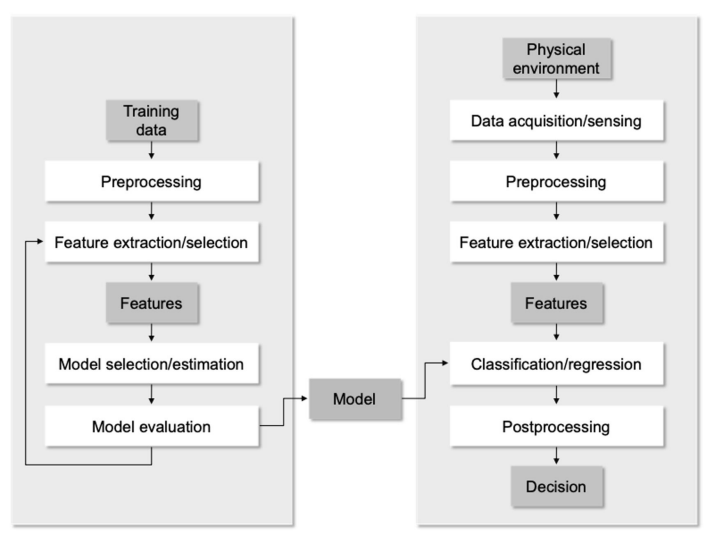
supervised

Unsupervised Learning

no output information for training data
- instead, we get ??truth values \(\Rightarrow\) just given input examples
Approaches:
- Clustering (K-Means, mixutre models, heirarchical)
- Hidden Markove Models (HMMs)
- Feature Extraction (PCA, iCA, SVD)
spontaneously finding ??patterns in input data like categorization
precursor to supervised learning
way to create higher-level represtation of data like automated feature extraction

Reinforcement Learning

when training data contain no correct output for each input (no longer supervised)
example: toddler learning not to touch a hot cup of tea
- training examples do not say what to do, still uses examples to reinforce better actions
- \(\Rightarrow\) learns what one should do in similar situations
training example의 target ouput X, but contains some possible output + measure of how good

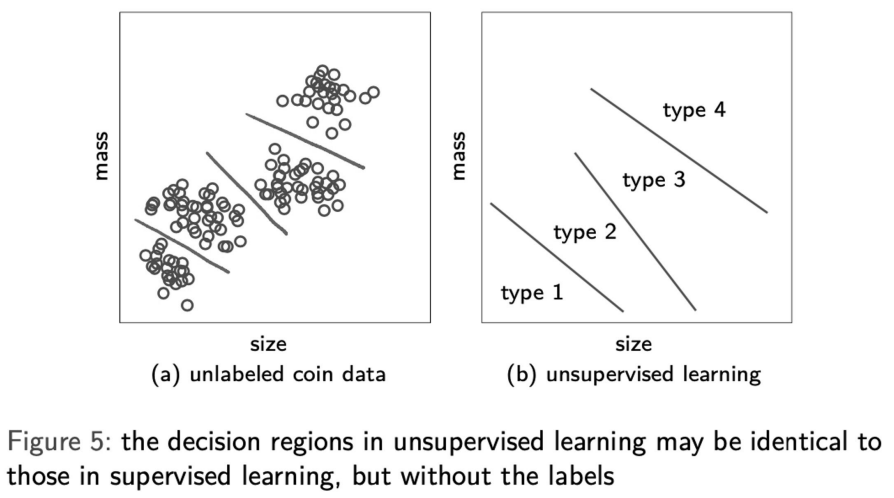
Supervised vs Unsupervised Example

supervised
unsupervised

Introduction

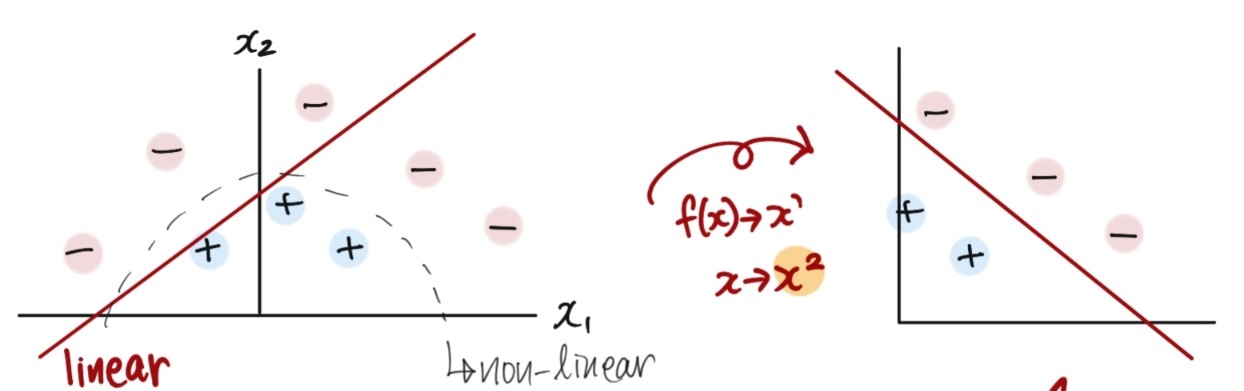
Core of Linear Models
- signal \(s = w^Tx\) : combines input variables linearly
Linear Regression
- \(signal = output\) for predicting real (unbounded) response
Linear Classification
- \(signal = threshold\) at zero to preduce \(\pm 1\) output, for binary decision
Logistic Regression aka Soft binary classification
- example: Heart attack precision based on cholesterol lvl, blood pressure, age, weight...
  - 확실하게 예측은 불가능, but can predict how likely it is
- binary decision (0 or 1) 보다 더 정교 \(\rightarrow\) 0 ~ 1 closer to 1 -> more likely to get 심장마비
- \(\Rightarrow\) output: real (like regression) but bounded (like classification)
- uncertain 가능
- more appropriate than linear regression (no negative values)

Predicting Probability

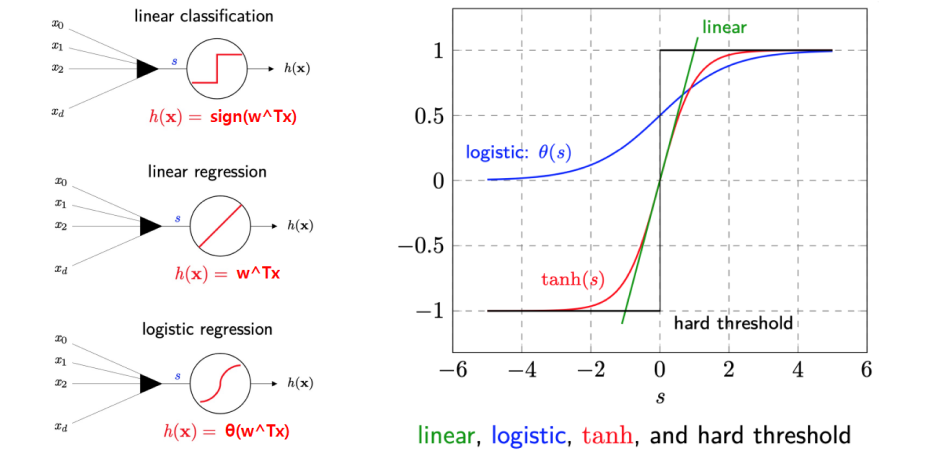
Logistic Regression Model

Linear Classification: hard threshold on signal \(s=w^Tx\)
\[h(x) = sign(w^Tx)\]
Linear Regression: no threshold
\[h(x) = w^Tx\]
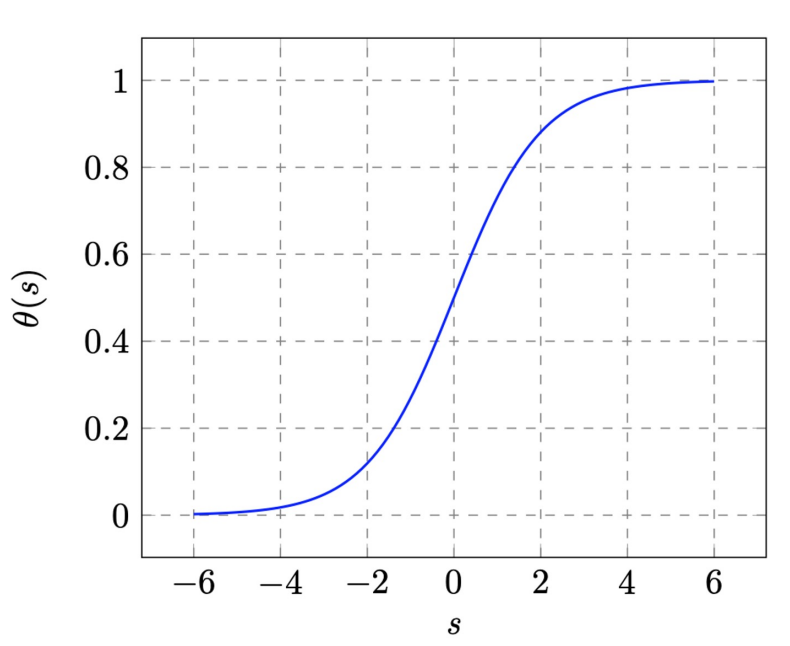
Logistic Regression between linear classification & regression
\[h(x) = \theta(w^Tx)\]
\(\theta\) : aka logistic function, Sigmoid function, soft threshold

Logistic Function θ

definition: for \(-\infty < s < \infty\) :
\[\theta(s) = \frac{e^s}{1+e^s} = \frac{1}{1+e^{-s}}\]

Proof

\[1-\theta(s) = 1- \frac{1}{1+e^{-s}} = \frac{e^{-s}}{1+e^{-s}} = \theta(-s)\]
\[\theta(s) = P(+1 \mid x)\]
\[P(-1\mid x) = 1-\theta(s) = \theta(-s)\]

output lies between 0 and 1 can be interpreted as probability for binary events
\(\theta(s)\) : can define error measure, has computational advantage

Summary of Linear Models

based on “signal” \(s = \sum_{i=1}^dw_ix_i\)

Hyperbolic Tangent (another popular sigmoid)

\[tanh(s)=\frac{e^s-e^{-s}}{e^s+e^{-s}}\]
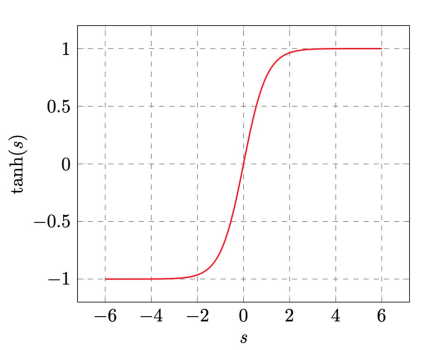
properties- \(tanh(s)\) convergence:
- large \(\mid s\) : hard threshold
- small \(\mid s\) : no threshold

linearsummary

example for heart attack:
- input x: cholesterol level, age, weight, etc..
- signal s = \(w^Tx\) : risk score
- Linear Classification: h(x) returns \(\pm 1\): heart attack (+1) or not (-1) for sure
- Linear Regression: h(x) returns risk score \(s\)
- Logistic Regression: h(x) returns \(\theta(x)\): probability of heart attack

Cross-entropy Error Measure

Learning Target of Logistic Reg

\[f(x) = \mathbb P [y= +1 \mid x]\]

ex : probability of heart attack given patient characteristics
training data doesn’t give us value of \(f\), rather, gives us samples generated by this probability \((+1 / -1)\)

Fitting

Fitting
: finiding a good \(h\)
\(h\) is good if \(\begin{cases} h(x_n) \approx 1 & y_n = +1 \\ h(x_n) \approx 0 & y_n = -1 \end{cases}\)
MSE works for linear models only, since it can fall into a local minimum
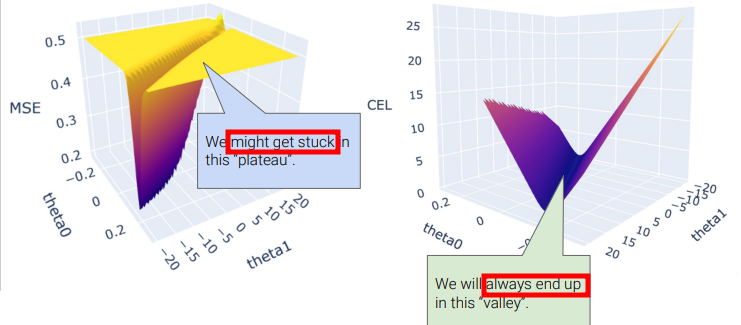
- if in the yellow area, it will get stuck and will not converge into local minimum
\(\Rightarrow\) use Cross-Entropy error measure

\[E_{in}(w) = \frac{1}{N}\sum_{n=1}^{N}ln(1+e^{-y_nw^Tx_n})\]

easier to do gradient-based optimization
\(y_n = +1\) encourages \(w^Tx_n >> 0 \longrightarrow \theta(w^Tx_n) \approx 1\) (and vice versa)

Error Measure

based on likelihood
how likely is it to get output \(y\) from input X
recall:
- \(h(x)\) = \(\theta(w^x)\)
- \(\theta(s)\) =\(\frac{e^s}{1+e^s}\)
- \(1-\theta(s)\)= \(\theta(-s)\)
\[P(y \mid x) = \begin{cases} h(x) & ,y = +1 & = \theta(w^Tx) \\ 1- h(x_n) &,y= -1 & = \theta(-w^Tx) \end{cases} \hspace{0.5cm} = \hspace{0.5cm} \theta(yw^Tx)\]
PROOF
- \(P(+1 \mid x)\) = \(h(x) = \theta(w^Tx)=\frac{1}{1+exp(-w^Tx)}\)
- \(P(-1 \mid x)\) = \(1-h(x) = 1-\theta(w^Tx)\)
  - 1- \(\frac{1}{1+exp(-w^Tx)}\)
  - \[\frac{exp(-w^Tx)}{1+ exp(-w^Tx)}\]
  - \(\Rightarrow\) \(\theta(-w^Tx)\)

Criterion for choosing h: maximum likelihood

\(\Rightarrow\) select hypothesis \(h\) that maximizes this probability
- \[P(y_1\mid x_1)P(y_1\mid x_2)\cdots P(y_N\mid x_N) \Longrightarrow \Pi_{n=1}^{N} P(y_n\mid x_n)\]
- getting all \(y_n\)’s from corresponding \(x_n\)’s
we can easily optimize/minimize if we change the maximum likelihood into log form
- \[-\frac{1}{N}ln(\Pi_{n=1}^{N} P(y_n \mid x_n)) = \frac{1}{N} \sum_{n=1}^N ln\frac{1}{P(y_n \mid x_n)}\]
- \(\Rightarrow\) negative log likelihood
- \(-\frac{1}{N}ln(\cdot)\) = monotonically decreasing function
\[\frac{1}{N} \sum_{n=1}^N ln\frac{1}{\theta(yw^Tx)}\]
- \[\frac{1}{N} \sum_{n=1}^N ln\begin{cases} h(x_n) & y_n = +1 \\ 1- h(x_n) & y_n = -1 \end{cases}\]
- \[\frac{1}{N} \sum_{n=1}^N {[\![ y_n = +1]\!] ln\frac{1}{h(x_n)} + [\![ y_n = -1]\!] ln\frac{1}{1-h(x_n)}}\]
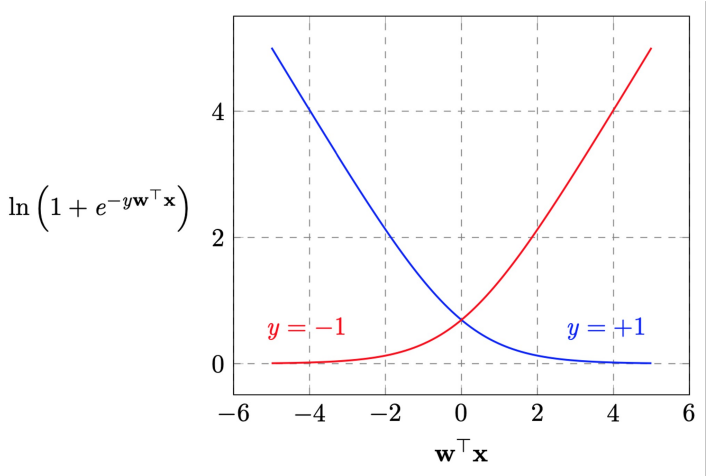
back to \(E_{in}(w) = \frac{1}{N}\sum_{n=1}^{N}ln(1+e^{y_nw^Tx_n})\)
Proof
- substituting \(\theta(yw^Tx)\), \(\frac{1}{N} \sum_{n=1}^N ln\frac{1}{\frac{e^{yw^Tx}}{1+e^{yw^Tx}}}\)
- = \(\frac{1}{N} \sum_{n=1}^N ln\frac{1+e^{yw^Tx}}{e^{yw^Tx}}\)
- = \(\frac{1}{N} \sum_{n=1}^N ln (1+e^{yw^Tx}) \cdot (e^{-yw^Tx})\)
- \[\frac{1}{N} \sum_{n=1}^N ln (1+e^{-yw^Tx})\]
- since \(e^0 = 1\)
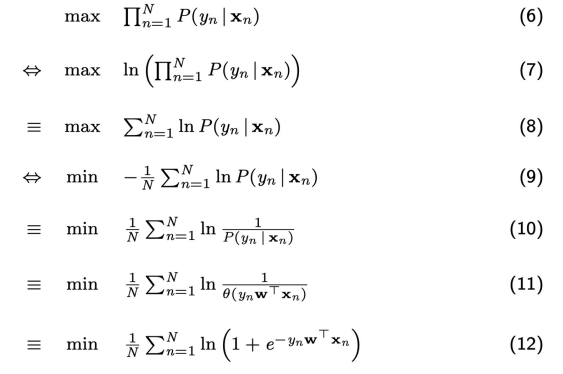
Practice Questions
1. Select the expression that describes the odds ration \(\frac{P(Y=1\mid X)}{P(Y=0\mid X)}\) of a logistic regression model. Recall: \(P(Y=0\mid X) + {P(Y=1\mid X)} = 1\) for any \(X\) and \(\theta(s) = \frac{1}{1+exp(-s)}\)
  - (a) \(X^Tw\)
  - (b) \(-X^Tw\)
  - (c) \(exp(X^Tw)\)
  - (d) \(\theta(X^Tw)\)
  - (e) None of these
2. Select the expression that describes \(P(Y=0\mid X)\) for a logistic regression model.
  - (a) \(\theta(-X^Tw)\)
  - (b) \(1-log(1+exp(X^Tw))\)
  - (c) \(1+log(1+exp(X^Tw))\)
  - (d) None of these
Answer
1. (c) 2. (a)

Training via Gradient Descent

update rule: \(w(t+1) = w(t) - \alpha \nabla E_{in}(w(t))\)
- \(\alpha\): learning rate (step size)
- \(E_{in}\): Training error
- examine all examples at each iteration: \(O(N)\)
- stochastic gradient descent : \(O(1)\)
Least Mean Square (LMS) rule (Windrow-Hoff learning rule)
- when the cost function is mean squared error
- \(w\): = \(w - \alpha \nabla E_{in}(w)\)
- = \(w + \alpha (y-w^Tx)\cdot x\)
  - \((y-w^Tx)\) : error
  - \(x\) : input

Logistic Regression Algorithm

intialize weights at time step t=0 to w(0)
for t = 0,1,2…do
\(\hspace{1cm}\)compute the gradient
- \[\nabla E_{in}(w(t)) = \frac{1}{N}\sum_{n=1}^N \frac{y_nx_n}{1+e^{y_nw^T(t)x_n}}\]
\(\hspace{1cm}\) set the direction to move: \(v_t = - \nabla E_{in}(w(t))\)
\(\hspace{1cm}\) update weights: \(w(t+1) = w(t) + \alpha(v_t)\)
\(\hspace{1cm}\) iterate to next step until it is time to stop
return final weights w

we have to choose 2 things:
1. initial weights w(0)
2. criterion for stopping gradient descent

Initialization Criterion

w(0) = 0
- works pretty well for logistic regressions
w(0) = random
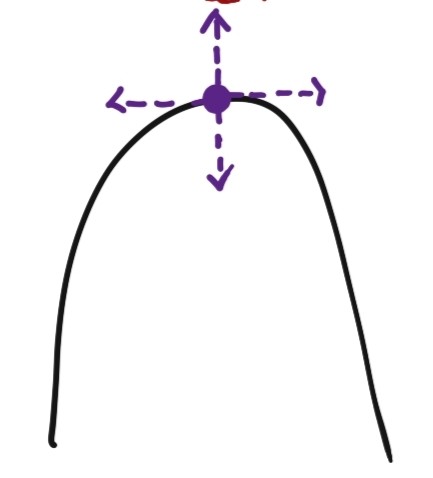
- more common, avoid getting stuck on perfectly symmetric hilltop
choose each weight independently from normal distribution with zero mean and small variance
- used pratically

Stopping

set upper bound on number of iterations
- PROBLEM: final weight quality not guaranteed
check gradient (\(\nabla E_{in}(w(t))\)) under threshold whenver loss function became too small
- PROBLEM: eventually must happen, but don’t know when
- PROBLEM 2: relying soley on size of gradient might stop too soon
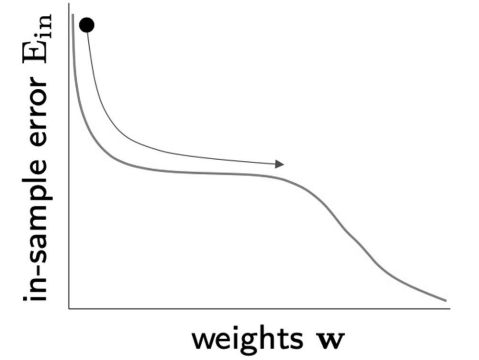
require both:
- (i): change in error is small
- (ii): error itself is small
- logistic regression: (1) + (2) works well
- (1) large upper bound for number of iterations
- (2) small lower bound for the size of gradient
```
  - ultimately, (1) + (2) + (3) is good
```

SUMMARY

summary1 summary2 summary3

Logistic Regression II

Thresholding

outputs of Logistic Regression : continous
Logistic Regression + Decision Rule = Classification
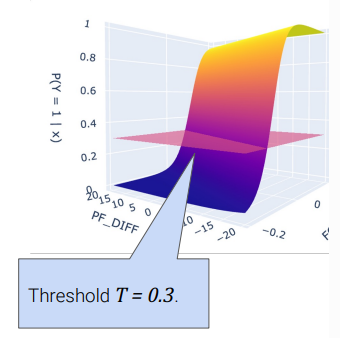
Decision Rule outputs 1 or 0 (depending on threshold)
- ex: \(T = 0.5\)
- \[classify(x) = \begin{cases} 1, & P(Y=1\mid x)>= 0.5 \\ 0, & P(Y=1 \mid x) < 0.5 \end{cases}\]
widely used in object detection

Thresholds for higher dimensions: also works fine

summary1

Evaluation Metrics

Accuracy

\[accuracy = \frac{ points \hspace{0.1cm} classified \hspace{0.1cm} correctly }{ total \hspace{0.1cm} points}\]

Pitfalls of Accuracy (Spam/Ham Classification)
- 100 emails, 5 = spam, 95 = ham, model classifies every email as ham
- accuracy : 95% (\(\frac{95}{95+5}%\)) \(\Rightarrow\) is it good enough?
  - NO: detecting spam email = 0%

Classification Errors

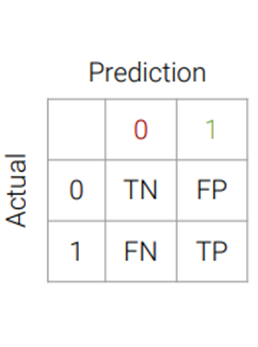
True Positives: correctly classified as positive
True Negatives: correctly classified as negative
False Positives: Mistakenly detected as positive (false alarm)
False Negatives: Failed to Detect

Precision and Recall

\[accuracy = \frac{TP + TN}{n}\]

What proportions of points did our classifier classify correctly?
- doesn’t tell full story, especially in cases with high class imbalance
- 정확도

\[precision = \frac{TP}{TP+FP}\]

Of all observations that were predicted to be 1, what proportion were actually 1?
- how precise is our classifier? Penalizes false positives
- 1으로 분류된 애들 중, 실제 1인 퍼센티지

\[recall = \frac{TP}{TP+FN}\]

Of all observations that were actually 1, what proprtion did we predict to be one?
- How good is our classifier at detecting positives? Penalizes false negatives
- 실제로 1인 애들 중, 1으로 분류된 퍼센티지
Filtering Spam Mails:
- 100 emails, 5 = spam, 95 = ham, model classifies every email as ham
- \(TP = 0\) , \(FP = 0\) , \(TN=95\), \(FN=5\)
- accuracy : 95% (\(\frac{95}{95+5}%\))
- precision: undefined (\(\frac{0}{0+0}%\))
- recall: 0% (\(\frac{0}{0+5}%\))
- \(\rightarrow\) accuracy does not tell full story
- \(\Rightarrow\) Class Imbalance: distribution of true observation is skewed (95% of true observations are negative)

Trade-off between precision and recall

100% recall : making ALL classifier output “1”
- no False Negatives, but many False Postives \(\longrightarrow\) precision low
\(\Rightarrow\) Precision and Recall inversly related
adjusting classification threshold
- higher
  threshold : \(\longrightarrow\) fewer FP, Larger Precision
- lower
  threshold : \(\longrightarrow\) fewer FN, Larger Recall

Questions:

In each of the following cases, what would we want to maximize: precision, recall, or accuracy?

1. Predicting whether or not a patient has some disease

Maximize RECALL : if they are told to have disease \(\rightarrow\) further testing
better than leaving them untreated

2. Determining whether or not someone should be sentenced to life in prison.

Maximize PRECISION : don’t want to sentence guilty people ??????????

3. Determining if an email is spam or ham

Maximize Accuracy : (subjective) having spam emails ending up at inbox, or hams being filter out 중 택1

Metrics

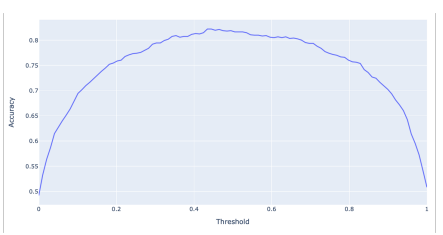
Accuracy vs. threshold

threshold \(\uparrow\) \(\longrightarrow\) Larger FN
threshold \(\downarrow\) \(\longrightarrow\) Larger FP
also, accuracy is maximized doesn’t always mean \(T\) = 0.5

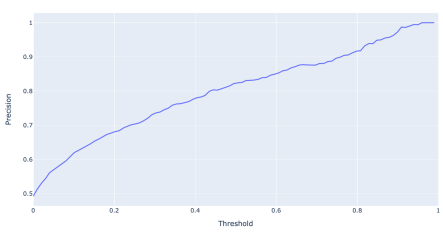
Precision vs. threshold

threshold \(\uparrow\) \(\longrightarrow\) Fewer FP
\(\Rightarrow\) precision increase
\(precision\) = \(\frac{TP}{TP+FP} = \frac{TP}{predicted \hspace{0.1cm}true}\)

Recall vs. threshold

threshold \(\uparrow\) \(\longrightarrow\) Larger FN
\(\Rightarrow\) recall decrease
\(Recall\) = \(\frac{TP}{TP+FN} = \frac{TP}{Actually \hspace{0.1cm}true}\)

Accuracy, Precision, Recall

Precision Recall Curves

threshold decrease: top left \(\longrightarrow\) bottom right
Perfect Classifier: precision = 1, recall = 1
- PR curve to be at top right of graph
Area Under Curve (AUC): optimal = 1 ROC more common

Other Metrics

False Positive Rate (FPR):
- \(\frac{FP}{FP+TN} \longrightarrow\) what proportion of innocent ppl did I convict?
True Positive Rate (TPR):
- \(\frac{TP}{TP+FN} \longrightarrow\) what proportion of guilty ppl did I convict? \(\Rightarrow\) RECALL

ROC Curves Receiver Operating Characteristics

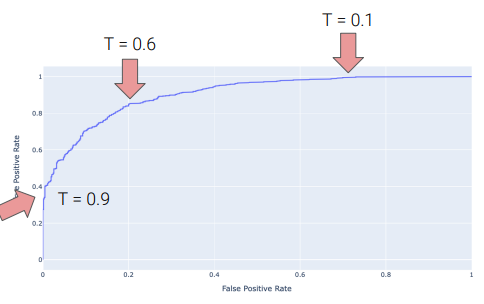
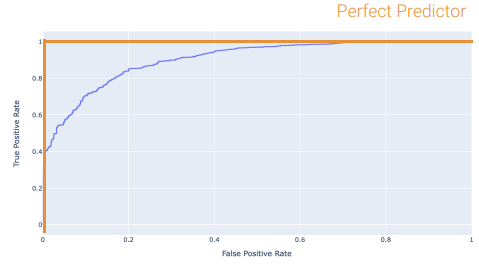
plots TPR vs FPR
threshold \(\uparrow\) \(\longrightarrow\) TPR & FPR decrease
- decreased TPR = bad (detecting fewer positives)
- decreased FPR = good (fewer false positives)
- \(\Rightarrow\) Tradeoff
Perfect classifier: TPR=1, FPR = 0, top-left
- best possible AUC = 1
- terrible AUC = 0.5 (randomly guessing)
- model’s AUC [0.5~1]

Feature Engineering

the process of transforming raw features into more informative features

feature

10년 전에 자주 사용한 기법, 이제는 DL 로 대체
enables to:
- caputure domain knowledge
- express non-linear relationships using simple linear models
- encode non-numeric features to be used as inputs to models

\[\hat y=f_{\theta}(x) = \sum^p_{j=0}\phi (x)_j\theta _j\]

phi

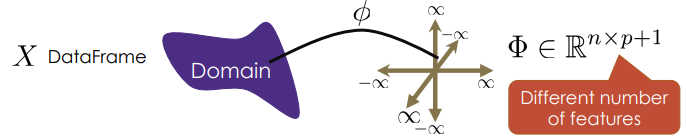
use \(\phi\) to transform features

Feature Functions Examples

Constant Feature Function: adding another vector as bias term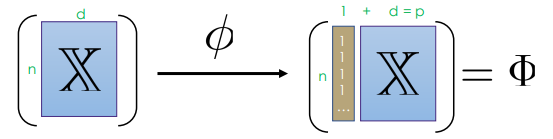
- aka constant feature, offset, intercept term, bias
Modeling Non-linear Relationships
- apply non-linear function
  (like \(sin()\)) \(\Rightarrow\) may be easier to optimize
- \[f_{\theta}(x) = \theta _0 + \theta _1 x_1 + \theta _2 x_2 + \theta _3sin(x_1+x_2)\]

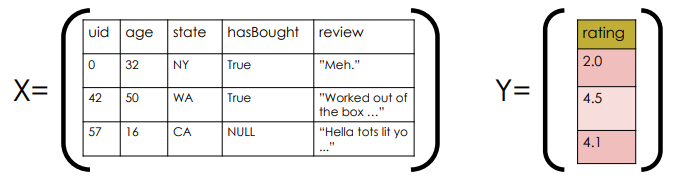
constant

cannot use \(X\) and \(Y\) in linear model because of text, categorical data, missing values …etc

Basic Transformations

Uninformative Features: like `UID`
- \(transformation\): Remove
Quantitative Features like `Age`
- \(transformation\): may apply non-linear transformations like Log
- \(transformation\): Normalize/Standardize like (x-mean)/stdev
Categorical Features like `State`
- simply assiging values (Alalbama=1, .., Utah=30) may indicate that those values have meaning (order / magnitude) NOT PREFERABLE
- \(transformation\): One-hot-Encode
Missing Values
- Quantitative:
1. estimate and fill in (tricky) like substituting mean
2. add another feature (boolean) named missing_col_name
  - sometimes missing data can be a signal

Categorical: (2) above (add additional category)

One hot Encoding (Dummy Encoding) 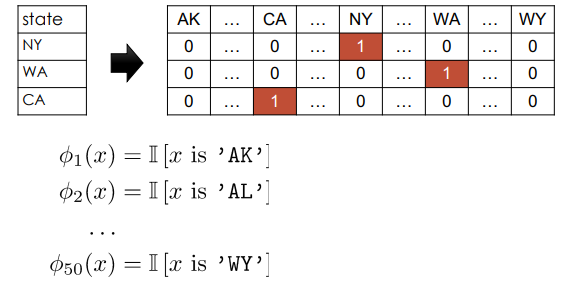constant

Bag of Words Encoding constant

bag: multiset (unordered collection which may contain multiple instance of each element)
stopwords typically removed
problems:
- too long and inefficient (high dimension but sparse)
- word order information lost (no context) \(\Longrightarrow\) N-gram
- new unseen words dropped \(\Longrightarrow\) add unkown_column for counting unseen words

N-Gram Encoding

when word order matters
problem: further inefficiency problem

Wrap up

feature transformations to capture domain knowledge
- introduces additional infromation
bag of words can be used in autocompletion

autocompletion

Feature Engineering Problems
- redundant features
- too many features
- overfitting