10 Optimization

in Notes / Dataanalytics / Datascience

Introduction

  • training

    most difficult optimization task

    • very important but very expensive (특수기술 필요)
  • examples:
    • training - learning optimal parameters (weights/biases) from data
    • model selection - tuning hyperparameters (ex: learning rate)
  • widely used:
    1. Stochastic Gradient Descent (SGD) and its variants
    2. Second-order methods
      • often too expensive to compute/store Hessian \(\Rightarrow\) memory-efficient tech emerging
    3. Convex Optimization (블록최적화): 중요하지만 DL에서 거의 쓸모X
  • Derivatives and Optimizaion Order
    • derivatives
      1. First Derivative (=gradient) \(\Rightarrow\) slope (Jacobian)
      2. Second Derivate \(\Rightarrow\) curvature (Hessian)
    • optimization
      1. First-order algorithms : use only gradient
        • \(x_{t+1}=x_t - \epsilon f'(x_t)\) supervised
      2. Second-order algorithms : also use Hessian matrix (aka Newton’s method)
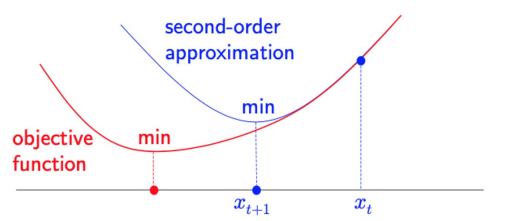
        • \(x_{t+1}=x_t - \frac{f'(x_t)}{f''(x_t)}\) supervised
  • Critical Points (stationary points)
    • points with zero slope: \(\nabla _x f(x) = 0\)
    • Derivative gives no info about which direction to move
    • Three types: maxima, minima, saddle point supervised
    • saddle point

      : both positive & negative curvature exist

      • \(f(x)\) \(=x_1^2-x_2^2\)
      • along \(x_1\) axis: \(f\) curves upward (local minimum)
      • along \(x_2\) axis: \(f\) curves downward (local maximum)
  • use of second derivative:
    1. characterize critical points
    2. measure curvature
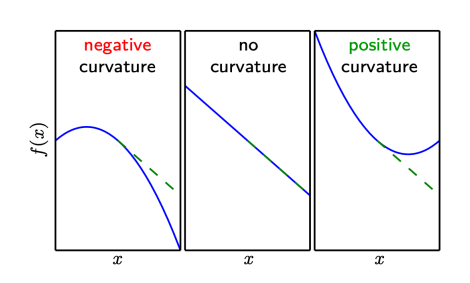
      • supervised
      • (i) negative curvature: \(f\) decreases faster than gradient predicts
      • (ii) no curvature: predicted correctly
      • (iii) positive curvature: \(f\) decreases slower than predicted \(\Rightarrow\) eventually increases
    3. predict performance of an update in gradient based opt.
  • In Deep Learning:
    • in high dimension: saddle points more common than local minima
    • obj function : many local minima + saddle points inside flat region \(\longrightarrow\) optimization difficult
    • \(\Rightarrow\) find a very low value of f (not necessarily minimal) supervised

Gradient-based Optimization

Gradient Descent and its Limitations

  • derivative: useful for minimizing a function
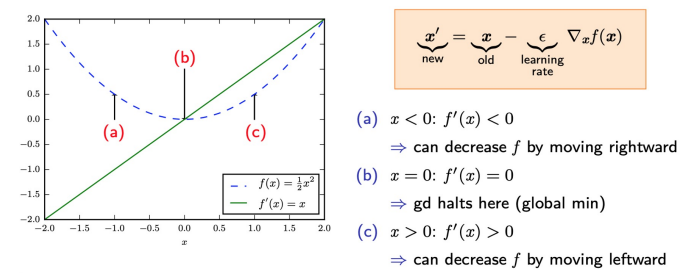
  • reduce \(f(x)\) by moving \(x\) in small steps with opposite sign of derivate supervised supervised
    • can obtain unbiased estimate of gradient ???
  • sgd and its variants (\(N\): total # of examples)
    1. \(m=1\): sgd
    2. \(1<m<N\) : mini-batch sgd (typical \(m\): 64, 128, 256, 512)
    3. \(m=N\): batch gradient descent

Properties of SGD

  • GOOD:
    1. number of training examples does not affect computation time per update
      • most important, allows convergence even with big # of examples
    2. SGD works better in practice than theory
  • BAD:
    1. Local minima and Saddle points
    2. Zero Gradient (Gradient descent gets stuck)
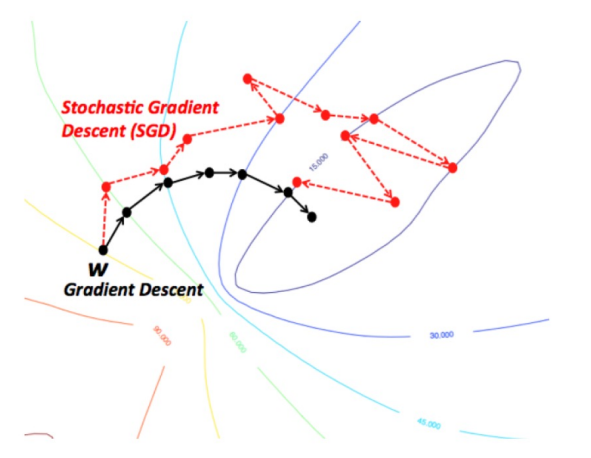
    3. Gradient Noise supervised
    4. Poor conditioning of \(H\)
  • Poor Conditioning of H
    • point \(x\) in multiple dimensions \(\rightarrow\) different second derivate for each direction
    • Condition Number

      of Hessian at \(x\) :

      how much second derivatives differ from each other

      • condition number of matrix with eigenvalues \({\lambda}\) : \(max_{i,j}\mid \frac{\lambda _i}{\lambda _j} \mid\)
    • if \(H\) have large condition # (poorly conditioned):
      1. Gradient Descent Performs poorly
        • 한쪽방향: deriv. increases rapdidly, 다른쪽: increase slowly
        • GD unaware of this change in the derivative
      2. Difficult to choose \(\epsilon\)
    • Example: Assume Hessian \(H\)’s condition number = 5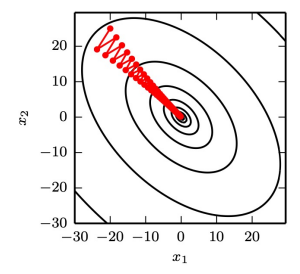
      • supervised
      • most curvature: 5 times more curvature than least (long canyon)
      • most curvature: direction \([1,1]\nearrow\)
      • least curvature: direction \([1,-1]\searrow\)
      • Gradient Descent (red lines): slow (zig-zag)
      • methods considering \(H\) : can predict: steepest direction not promising
      • \(\Rightarrow\) how to handle poor conditioning without directly considering \(H\)?

Exponentially Weighted Average (EWMA)

  • Given: time series \(g_1, g_2, \cdots\), EWMA : \(v_t = \begin{cases} g_1 & t=1 \\ \alpha v_{t-1}+(1-\alpha)g_t & t> 1\end{cases}\)

  • \(v_t\): EMWA at time \(t\)
  • \(g_t\): observation at time \(t\)
  • \(\alpha \in [0,1]\): degree of weighting decrease (constant smoothing factor, 주로 0.9)
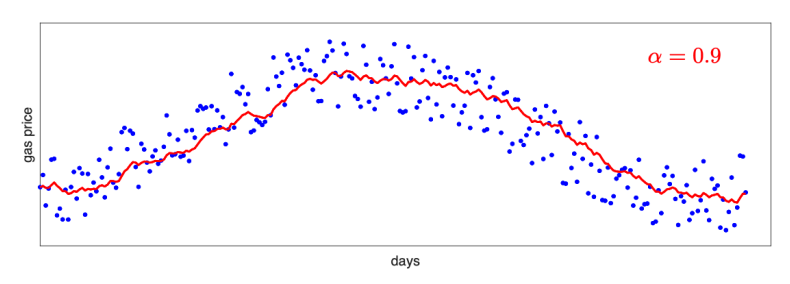
  • Example: gas price over time supervised
    • \(v_t\) \(= \alpha \cdot\) \(v_{t-1}\) \(+(1-\alpha) \cdot\) \(g_t\)
    • blue dots: gas price g
    • red curve: EWMA v
  • Effective weighting decreases exponentially over time:
    • \(v_t\) \(=\alpha v_{t-1}+(1-\alpha)g_t\)
    • = \(\alpha[\alpha v_{t-2}+(1-\alpha)g_{t-1}] +(1-\alpha)g_t\)
    • \(=\) …

    • \(=\alpha ^k v_{t-k}+(1-\alpha)\) \([g_t + \alpha g_{t-1}+\alpha ^2 g_{t-2}+\cdots+a^{k-1}g_{t-k+1}]\)

    • \(\Rightarrow\) “exponentially weighted” (최근 데이터에 더 많은 가치를 두고 제일 옛날꺼에는 거의 안둠)
  • Approximation:
    • \(v_t\) \(=(1-\alpha)g_t + \alpha v_{t-1}\)
    • \(=(1-\alpha)\) \([g_t + \alpha g_{t-1}+\alpha ^2g_{t-2} + \alpha ^3 g_{t-3} + \cdots]\)
    • \(=\frac{g_t + \alpha g_{t-1}+\alpha ^2g_{t-2}+\cdots}{1+\alpha + \alpha ^2 + \cdots} \Rightarrow\) weighted average formula
    • DENOMINATOR = effective number of observations:
      • \(1+\alpha + \alpha ^2 + \cdots\) = \(\frac{1}{1-\alpha}\)
    • bottom line : \(v_t \approx\) average over \(\frac{1}{1-\alpha}\) last time points
      • ex) \(a=0.9\) : average over 1/(1-0.9) = 10 points
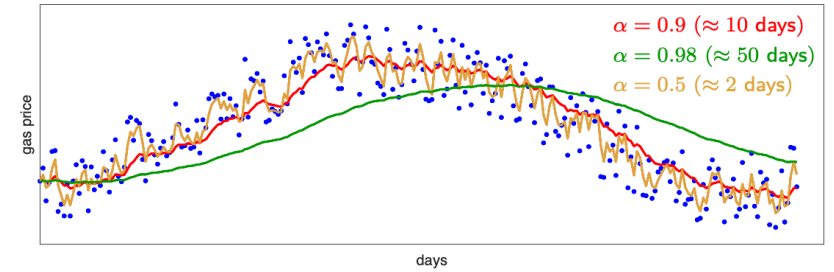
  • Effect of Smoothing Factor supervised
    • Higher \(\alpha \Rightarrow\) more weight to past, less weight to present
      • Smoother Curve \(\leftarrow\) averaging over more days
      • Shifted further \(\leftarrow\) averaging over larger window
      • Curve adapts more slowly to changes with more latency
  • Bias Correction
    • 첫 몇개의 샘플은 충분한 데이터가 안 쌓였기 때문에 inaccurate average
    • supervised
    • instead of \(v_t\), use \(\frac{v_t}{1-\alpha ^t}\)

Gradient Descent with Momentum

  • sgd: popular but sometimes slow
  • method of momentum (Polyak, 1664):
    • designed to accelerate learning, even though
      • high curvature
      • small but consistent gradients
      • noisy gradients
    • can be combined to existing sgd variants
  • Common Algorithm: accumulates exponentially decaying moving average of past gradients \(\rightarrow\) continue to move in that direction
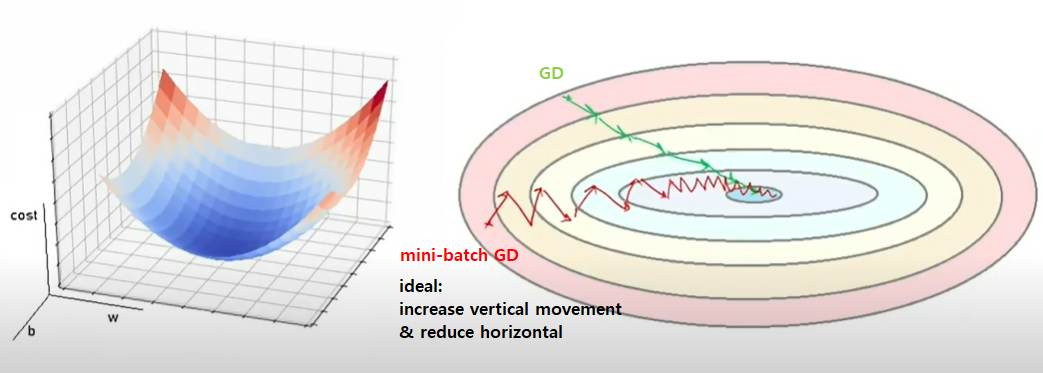
  • supervised

  • Momentum applied to three forms of SGD

    supervised

    • \(\theta\) updated by linear combination of gradient and velocity
    • \(\theta \leftarrow \theta - \epsilon(\) \(g\)\(+ constant \cdot\) v \()\)

Nesterov Momentum

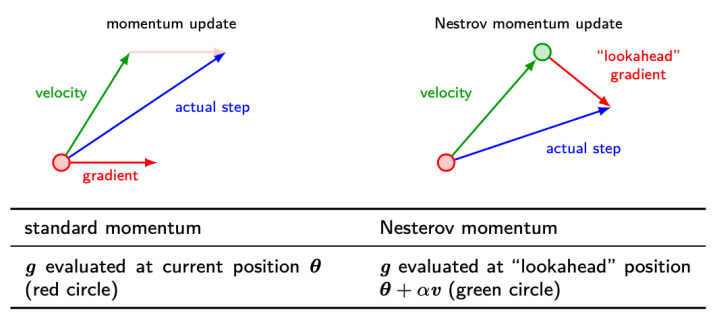
  • difference : nestrov
  • standard: gradient \(g = \nabla _\theta J\) evaluated at current position \(\theta\) (red circle)
  • Nestrov: \(g\) evaluated at lookahed position \(\theta + \alpha v\) (green circle), after current velocity is applied
    • \(\Rightarrow\) add correction factor
    • \[v \leftarrow \alpha v - \epsilon \nabla _\theta J(\theta + \alpha v)\]
    • \[\theta \leftarrow \theta + v\]
  • Advantages:
    1. Stronger theoretical converge guarantees for convex functions
    2. Standard Momentum보다 나음

Per-parameter Adaptive learning Rates

  • adaptively turn \(\epsilon\) for each parameter
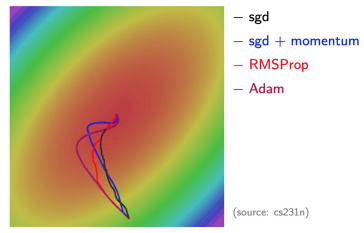
  • nestrov
  • nestrov
  • goal: move horizontally BUT huge vertical oscillations
  • \(\Rightarrow\) Solution: slow down learning vertically, speed up (적어도 유지) horizontally
  • 실제 구현 방법 (without relying on \(H\))

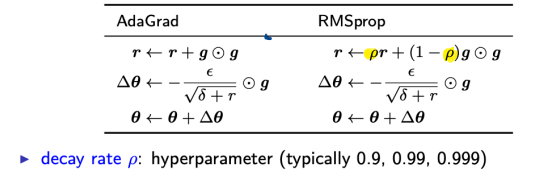
1. AdaGrad

  • individually adapts learning rate of each direction (each parameter)
    • steep direction: slow down learning
    • gently sloped direction: speed up learing
  • adjusts learning rates per parameter:
    • \(\epsilon _j =\) \(\frac{\epsilon}{\sqrt{\sum_{all \hspace{0.1cm}previous \hspace{0.1cm}iterations}(g_j \cdot g_j)}}\)
    • \(\epsilon\): global learning rate
    • \(\epsilon _j\): learning rate of dimension \(j\) (parameter \(\theta _j\) )
    • \(g_j = \frac{\partial J(\theta)}{\partial \theta _j}\) : gradient wrt dimension \(j\)
  • GOOD: greater progress in more gently sloped directions
  • BAD (esp in DL): monotonically decreasing \(\epsilon\): too aggressive + stops learning too early
  • Adadelta: extension of Adagrad
    • restricts accumulated past gradients
    • reduces aggressive \(\epsilon\)

2. RMSProp

root-mean-squaure prop

  • modified AdaGrad (non-convex setting에서도 잘 돌아가게)
  • Change gradient accumulation to EWMA
  • exponentially decaying average (\(\rho\)) 사용
    1. 아주 오래된 history 삭제
    2. converge rapidly after finding convex bowl

nestrov

3. Adam

adaptive moment estimation (RMSProp + momentum + bias correction)

  • for each iteration:
    1. compute gradient \(g\)
    2. update first moment: \(s \leftarrow \rho _1 s+(1- \rho _1) g \hspace{2cm} \leftarrow\) “momentum”
    3. update second moment: \(r \leftarrow \rho _2 s+(1- \rho _2) g \bigodot g\hspace{2cm} \leftarrow\) “RMSProp”
    4. bias correction: \(\hat{s} \leftarrow \frac{s}{1-\rho _1 ^t}, \hspace{2cm} \hat{r} \leftarrow \frac{r}{1-\rho _2 ^t}\)
    5. update parameter: \(\theta \leftarrow \theta - \epsilon \frac{\hat{s}}{\sqrt{\hat{r}+\sigma}}\)
Full algorithm

nestrov

  • often works better than RMSProp, recommened as default
  • sgd + Nestrov Momentum도 해볼만 함

Second-order Optimization

Idea behind Newton’s Method

  • considering Taylor Series approximation: \(f(x) \approx f(x^{(0)})+(x-x^{(0)})^Tg + \frac{1}{2}(x-x^{(0)})^TH(x-x^{(0)})\)
  • gradient: \(f'(x)\)
  • Hessian: \(f''(x)\)
  • at point \(x_0\):
    • \(f(x) \approx f(x_0) + (\) \(x\) \(-x_0)f'(x_0) + \frac{1}{2}(\) \(x\) \(-x_0)^2f''(x_0)\)
    • \(f'(x)\) \(=f'(x_0)+(x-x_0)f''(x_0)\) respect to x
    • \(0 = f'(x_0) + (x-x_0) f''(x_0)\) set to zero
    • \(0 = f'(x_0) + xf''(x_0) - x_0f''(x_0)\) solve for x
    • \(xf''(x_0) =\) \(x_0f''(x_0)-f'(x_0)\)
    • \[x= x_0 - \frac{f'(x_0)}{f''(x_0)}, \hspace{1cm} \longrightarrow x_0 - \frac{g}{H}\]

  • Newton’s Update Rule : \(x^* = x^{(0)}-\) \(H^{-1}\)\(g\)

    • PROS: No hyperparameter (in theory)
      • gradient requires \(\epsilon\) (hyperparameter) but this doesn’t
    • CONS: Inefficiency (\(H : O(n^2)\) elements, \(H^{-1}\) takes \(O(n^3)\) for inverting) \(\Rightarrow\) 안쓰는 이유
  • IDEA:

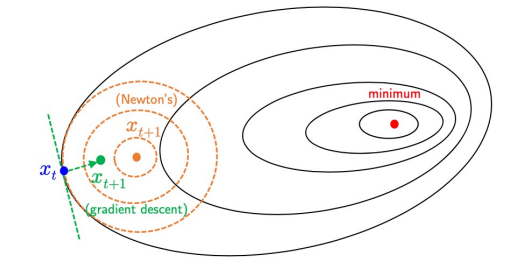
nestrov

  • get second-order approximation and minimize \(\Rightarrow\) faster than GD

Quasi-Newton Methods

  • avoid directly inverting \(H\) \(\rightarrow\) reduce comparison time (\(O(n^3) \rightarrow O(n^2)\))
  • approximate \(H^{-1}\) with Matrix \(M_t\)
    • \(M_t\): iteratively refined by low-rank updates
    • determine direction of descent by \(\rho _t = M_tg_t\) and update: \(\theta _{t+1} = \theta _t - \epsilon \rho _t\)
  • BFGS algorithm (Broyden-Fletcher-Goldfarb-Shanno)
    • most popular quasi-Newton method
    • still requires \(O(n^2)\) memory to store \(H^{-1}\)
  • L-GFGS (limited memory BFGS): doesn’t form / store full \(H\)
    • full batch / deterministic mode: usually GOOD
    • minibatch / stochastic setting : BAD

Summary

summary