05 Visualization

in Notes / Dataanalytics / Datascience

Introduction

  • Visualization

    use of computer-generated, interactive, visual representations of data to amplify cognition finding artificial memory that best supports our natural means of perception

  • visualizations are for humans (take advantage of human visual perception system)
Visualize, then quantify!

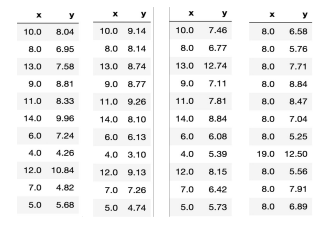
dataset

  • all four dataset have the same mean, standard deviations, and correlation \(\rightarrow\) same regression line!

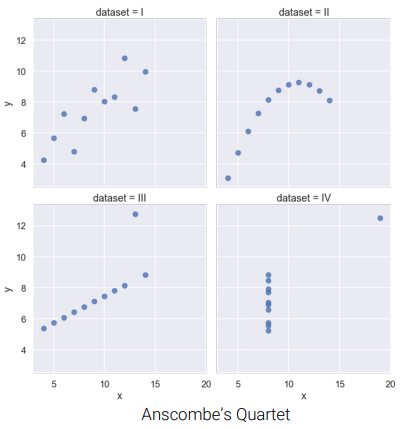
example

  • yet their graph look very different
  • \(\Rightarrow\) Visualization complements statistics
  • Goal of Data Visualization
  1. To help your own understanding of data/results
    • key part of EDA, useful throughout modeling
  2. To communicate results/conclusions to others
    • minimize explanations
  3. Inform human decisions
    • every visualizations have tradeoffs

Encoding

  • encoding: \(variable \longrightarrow\) map \(visual\) \(element\)

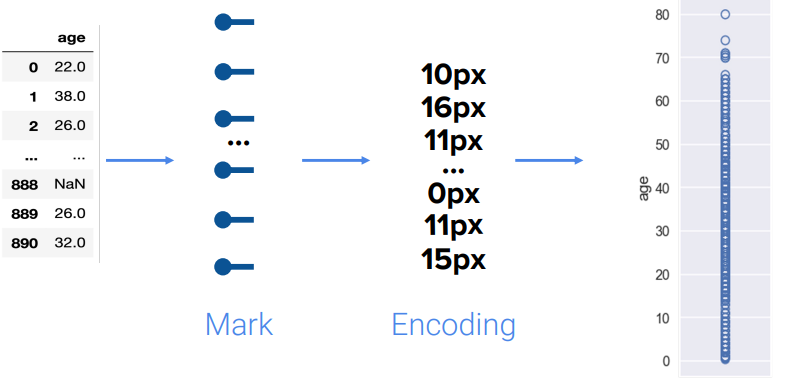
example

  • mark: represents a datum

  • \(Q\) : How many variables are we encoding here?

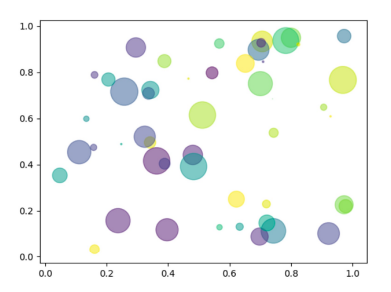
    example

    Answer
    • \(4\) variables
    1. x
    2. y
    3. area
    4. color

  • \(Q\) : What is wrong with this visualization?

    example

    Answer
    • incorrect use of bar chart
    • qualitative data used (Nationality) instead of quantitative
    • \(\Rightarrow\) not all encoding channels are exchangeable

Distribution

  • distribution

    : describes frequency at which values of variable occur

  1. show percentages (distrubtion) of category
  2. all values must be accounted for once and only once

  • \(Q1\) : Does this chart show a distribution?

    example

    Answer
    • NO
    • individuals can be in more than one category
    • numbers and bar length correspond to time, not proportion or number of individuals in category

  • \(Q2\) : Does this chart show a distribution?

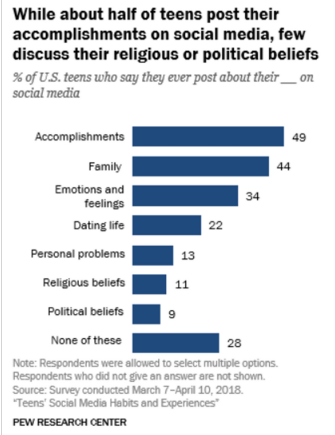
    example

    Answer
    • NO
    • does show percentages of individuals in different categories
    • BUT individuals can be in more than one category

  • \(Q3\) : Does this chart show a distribution?

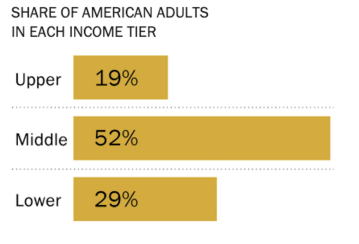
    example

    Answer
    • YES!
    • shows the distribution of the qualitative ordinal variable “income tier.”
    • Each individual is in exactly one category
    • The values we see are the proportions of individuals in that category
    • Everyone is represented, as the total percentage is 100%.

Type of Visualizations

Bar plots

  • most common way for qualitative (categorical) variable

  • also works for numerical variables on different categories

  • not a distribution, but still makes sense

  • length encode values

    • width = nothing
    • colors = may indicate sub-category

  • Ways to plot:

    1. matplotlib plt : basis of all three
    2. pandas .plot() : can make default plots
    3. seaborn sns : allow sophisticated visualizations quickly
  • births['Maternal Smoker'] = series of boolean values
    births['Maternal Smoker].value_counts().plot( kind = 'bar' )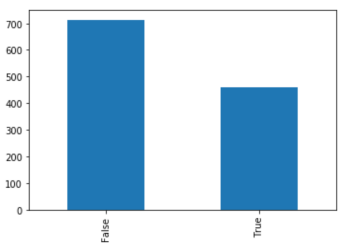

    example

    sns.countplot( births['Maternal Smoker'] )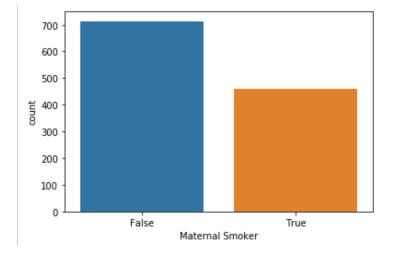

    example

  • list of majors and list of corresponding GPA
    • plt.bar( majors, gpas ) (horizontal: change bar \(\rightarrow\) barh)
    • sns.barplot( majors, gpa )
    result

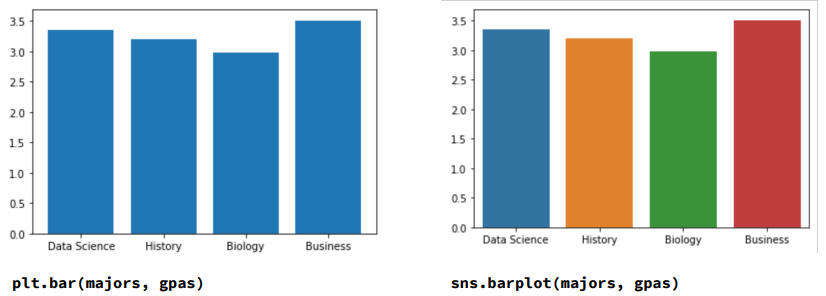
    example

    • here, the color is meaningless

Rug plots, Histograms, Density Curves

  • Rug Plots

    • for quantitative (numerical) varibles
    • shows each and every value
    • issues:
      • too much detail
      • hard to see bigger picture
      • Overplotting (ex: birthweights at 120: can’t tell, all on top of each other)
    • sns.rugplot(bweights)

  • Histograms

    • smoothed version of rug plot (lose granularity, gain interpretability)
    • horizontal axis \(\leftrightarrow\) : divided into bins
      • proportion in bin = width of bin * height of bin
    • area: proportions (total area = 1 (100%))
    • units of height: proprtion per unit on the x-axis
      plt.hist( bweights, bins=bw_bins, ec='w')
      • where bw_bins = range(50, 200, 5)

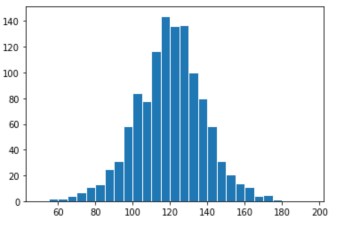
      example

      • \(\Rightarrow\) by default, matplotlib show counts on y-axis, instead of proportions per unit
      plt.hist( bweights, density=True, bins=bw_bins, ec='w')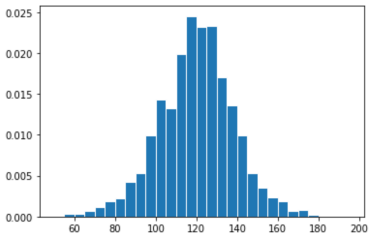

      example

      • \(\Rightarrow\) total area sums to 1 (y-axis fixed)

    • \(Example\)
      example

      • \(\approx\) 120 babies born with weight between 110~115 (y-axis = count)
      • total 1174 observations (given)
      • looking at y-axis=proportion graph:
        • width of bin [110, 115) = \(5\)
        • Height of bar [110, 115) = \(0.02\)
        • proportion of bin = 5 * 0.02 = \(0.1\)
        • Number in bin = 0.01 * 1174 = \(117.4\) \(\approx\) 120!
    • beware of drawing strong conclusions from looks of histogram
      • Number of bins influences appearance!
      • Freedman-Diaconis rule: \(Bin width = 2\frac{IQR(x)}{\sqrt[\leftroot{10} \uproot{5} 3]{n}}\)
    • Bins don’t need to to have the same width
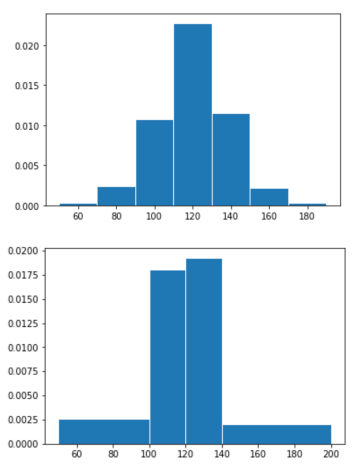
      • \(\Rightarrow\) especially crucial to think of proportions as areas example

  • Density Curves

    • instead of discrete histogram, visualize by continuous distribution
    • sns.histplot(bweights, kde=True)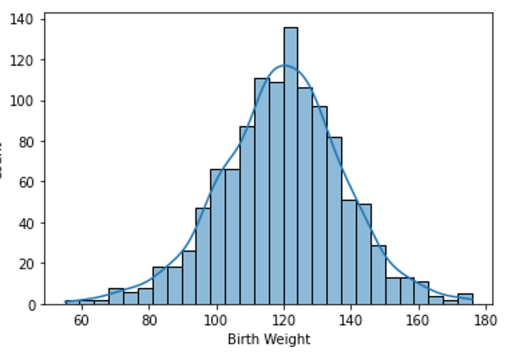 example
    • Desity Curve only
      sns.displot(bweights, kind='kde')
      • or sns.kdeplot(bweights) example

Describing Quantitative Distributions

  • Mode of distribution : local or global maximum
    unimodal, bimodal, multimodal

    example

  • Skew and Tails:

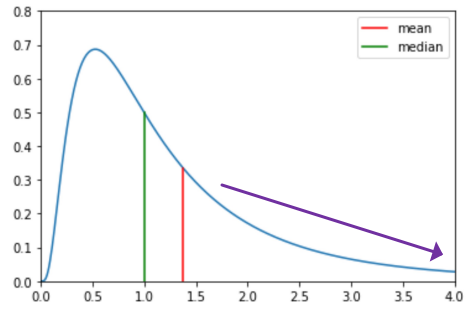
    • ex) long right tail = “skewed right” example
    • mean : balancing point of density
    • skewed right = median < mean
    • symmetric: both tails are equal size

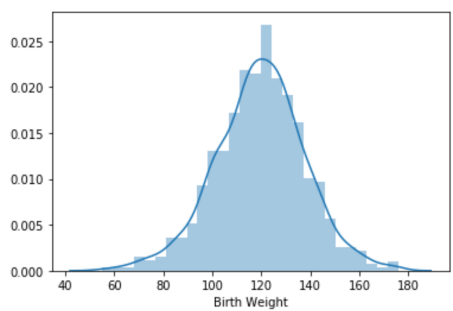
    example

    • unimodal and symmetric, roughly normal
  • Outliers

Box Plots and Violin Plots

  • Quartiles

    • 25th percentile: First/Lower quartile
    • 50th percentile: Second quartile (median)

    • 75th percentile: Third/Upper quartile

    • \(IQR\) (Interquartile Range) = third quartile - first quartile
      • measures spread

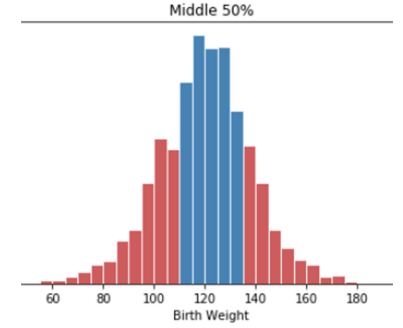
    example

  • Box Plots

    • sns.boxplot( bweigths )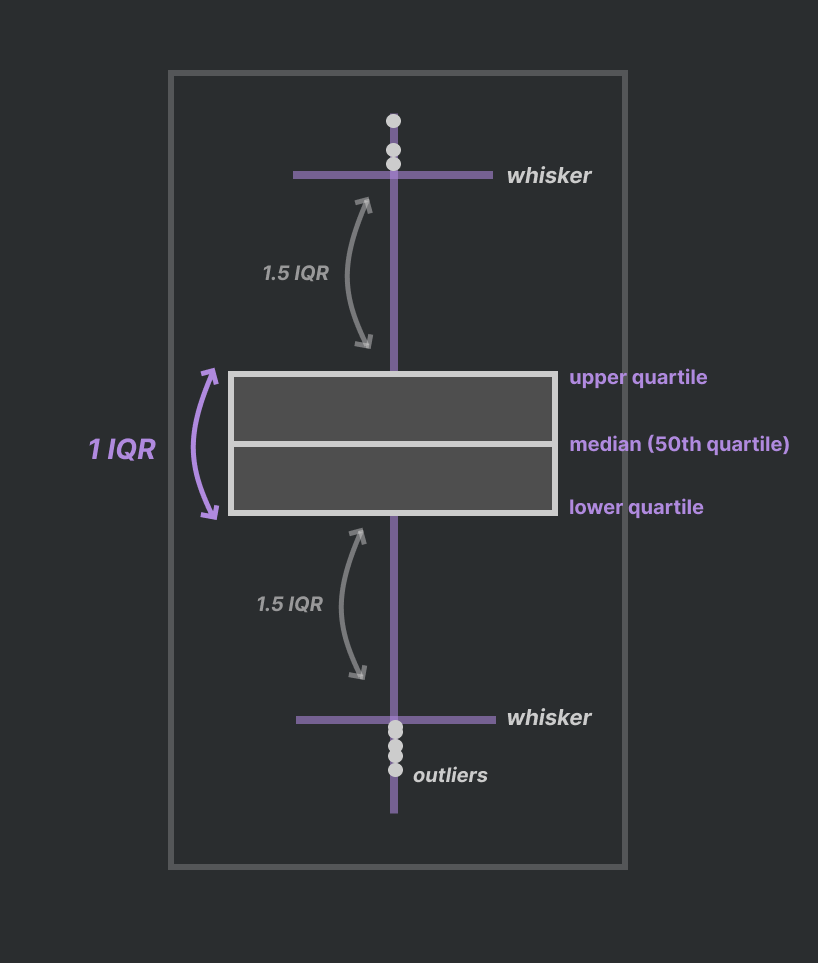 example
    • 참고: box width means nothing
      check by coding
      q1 = np.percentile( bweights, 25 )
q2 = np.percentile( bweights, 50 )
q3 = np.percentile( bweights, 75 )
iqr = q3 - q1
whisk1 = q1 - ( 1.5 * iqr )
whisk2 = q4 + ( 1.5 * iqr )

whisk1, q1, q2, q3, whisk2
>>> (73.5, 108.0, 120.0, 131.0, 165.5)

  • Violin Plots : box-whisker + density curve

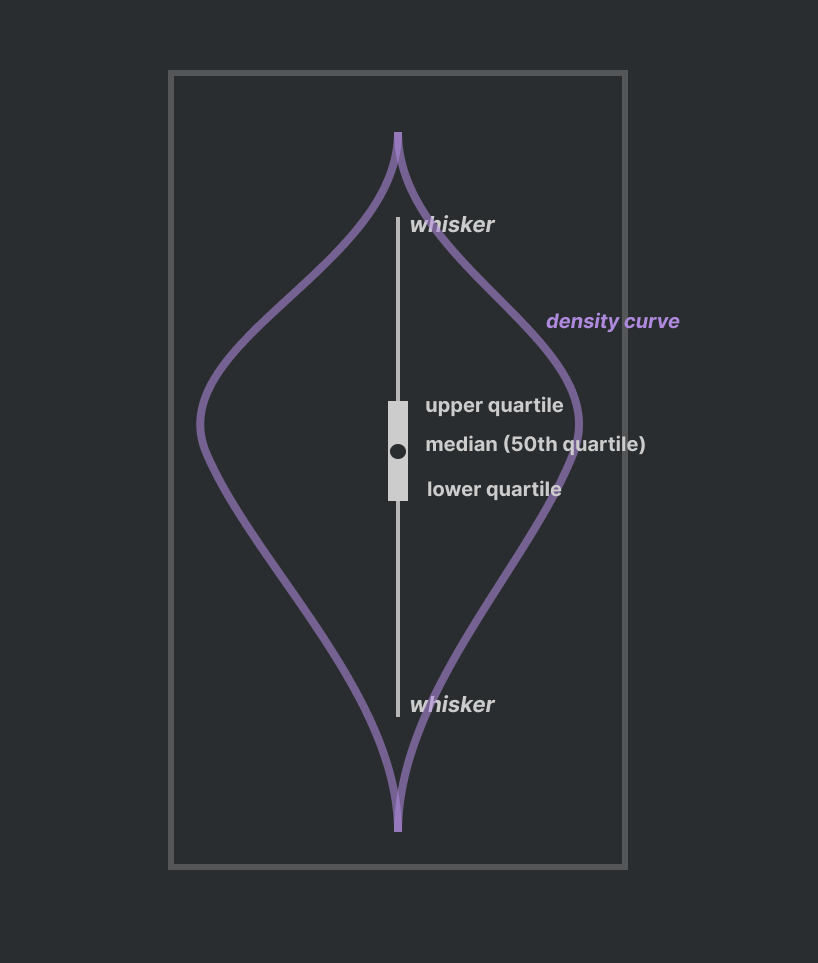
    example

    • width have meaning

Comparing Quantitative Distributions

  • Overlaid histograms and density curves:

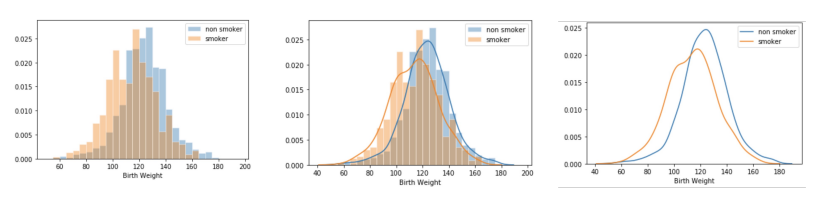
    example

    • First graph: not bad but looks like 3 seperate histograms
    • Second graph: too much information and unclear
    • Third: although estimates are rough, it’s the best

  • Side by side box plots and violin plots:

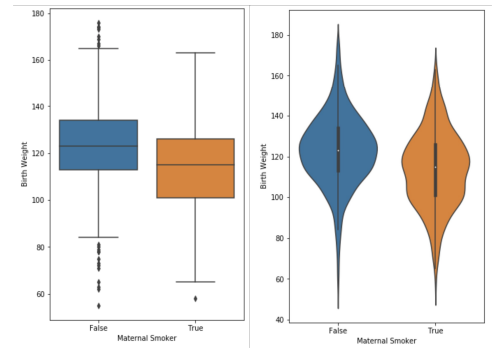
    example

    • concise, well suited side by side
    • violin plot shows us bimodal nature of True category

Relationships between two quantitative variables

  • Scatter plots: used to reveal relationship between pairs of numerical variables

    • help inform modeling choices example

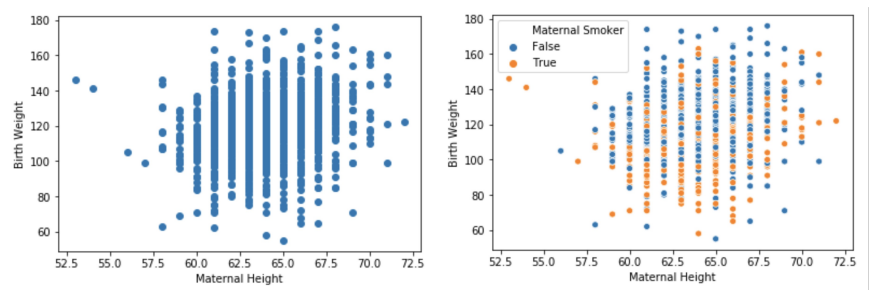
    • color usage also helpful example
    • overplotting : points on top of each other
      • \(\Rightarrow\) use random noise in both x y directions \(\begin{bmatrix} 65 & 170 \\ 65 & 170 \\ ... \end{bmatrix} \rightarrow \begin{bmatrix} 65^{+0.2} & 170^{+0.2}\\ 65^{-0.2} & 170^{-0.2}\\ ... \end{bmatrix} \Rightarrow \begin{bmatrix} 65.2 & 170.2\\ 64.8 & 169.8\\ ... \end{bmatrix}\)
      • \(\Rightarrow\) change in shape, but clearer
    sns.lmplot(data=births, x=‘Maternal Height’, y=‘Birth Weight’, ci=False)
    - or `sns.jointplot(data=births, x=‘Maternal Height’, y=‘Birth Weight’)`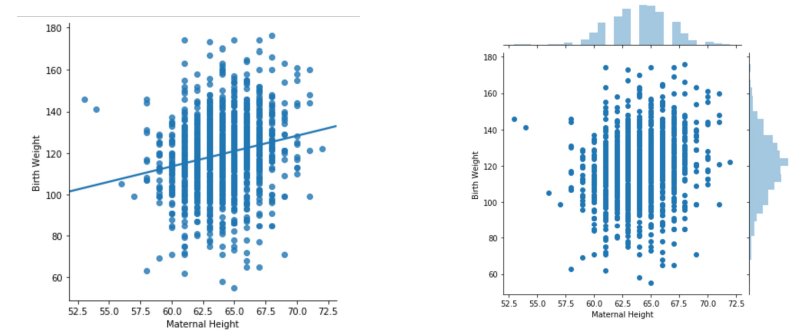

    example

  • Hex plots:

    • \(\approx\) 2-D histogram
    • shows joint distribution
    • xy plane binned into hexagons
    • darker (more shaded) \(\rightarrow\) greater density/frequency
    • Why hexagons ⬡ instead of squares □?
      • easier to see linear relationships
      • more efficient for covering region
      • visual bias of squares (tend to see ver, hori lines)
      sns.jointplot(data=births, x=‘Maternal Height’, y=‘Birth Weight’, kind=’hex’)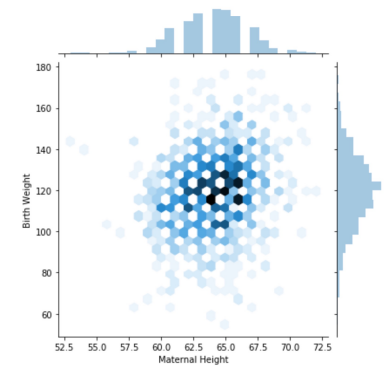

      example

  • Contour plots:

    • \(\approx\) 2-D versions of density curve
    • default: shows marginal distributions on the horizontal and vertical axes.
    • \(\Rightarrow\) histograms/density curves of each variable independently
    sns.jointplot(data=births, x=‘Maternal Height’, y=‘Birth Weight’, kind=’kde’, fill=True)
    <img src="../DataAnalytics/DataScience/assets/5-contourplot.png" alt="example" style="height: 300px; width: auto;"/>

Principles of Visualization

Scale

  • case study: Planned Parenthood accused of selling aborted fetal tissues for profit.
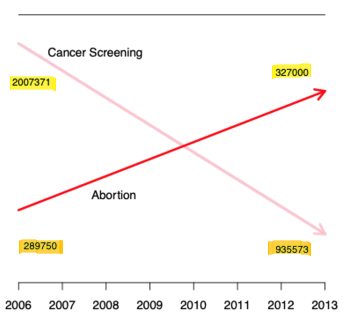
    • below graph presented by Congressman Chaffetz (from another report) example
    • \(\Rightarrow\) Misleading; Do not use two different scales for the same axis!
    Visualization with correct scale

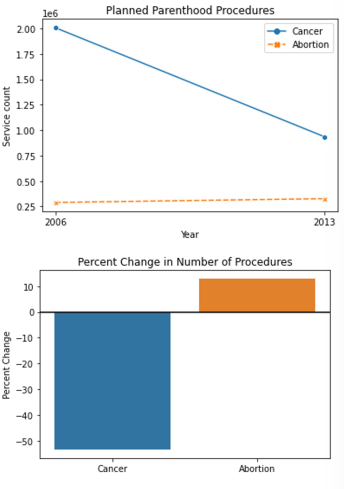
    example example - \(\Rightarrow\) Abortions increased from 13% to 26% of total procedures.

  • Reveal the data
    • choose axis limits to fill the visualization
    • if necessary: zoom in on the bulk of data
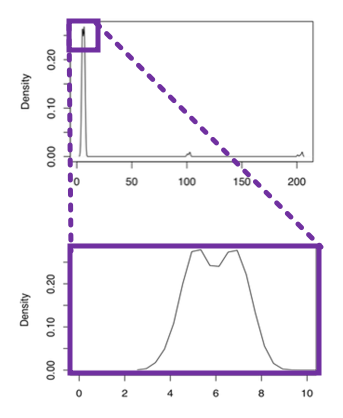
    • create multiple plots to show different regions of interest example

Conditioning

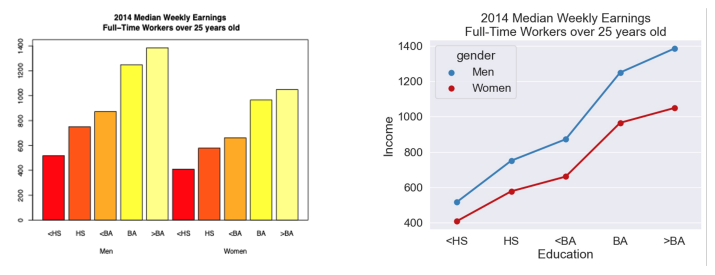
  • case study: median weekly earnings example

    • \(\Rightarrow\) right is more clear

  • Distributons and relationships in subgroups

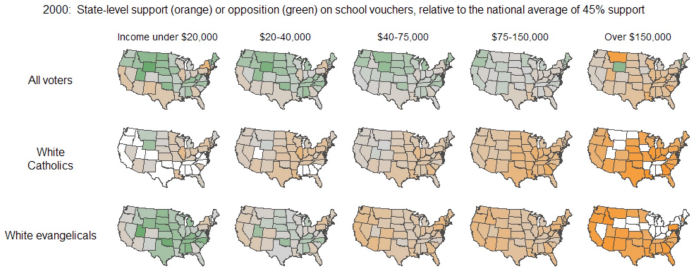
    • Juxtaposition: placing multiple plots side by side with same scale (‘small multiples’) example

    • Superposition: placing multiple densitiy curves, scatter plots on top of each other
    • use color and shapes to reperesent additional variables

Perception

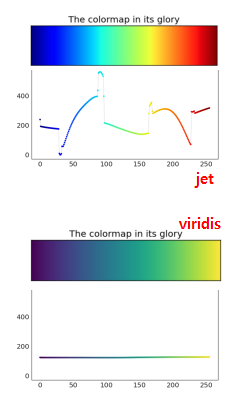
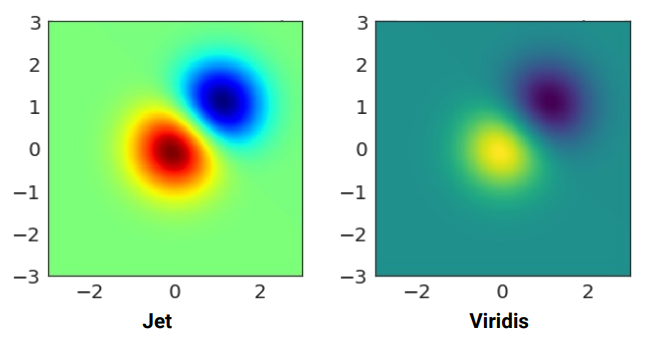
  • Colors example

    • jet: boundary (old matplotlib default colormap)
    • viridis: continuous change (current matplotlib default)
    Jet/rainbow colormap misleads

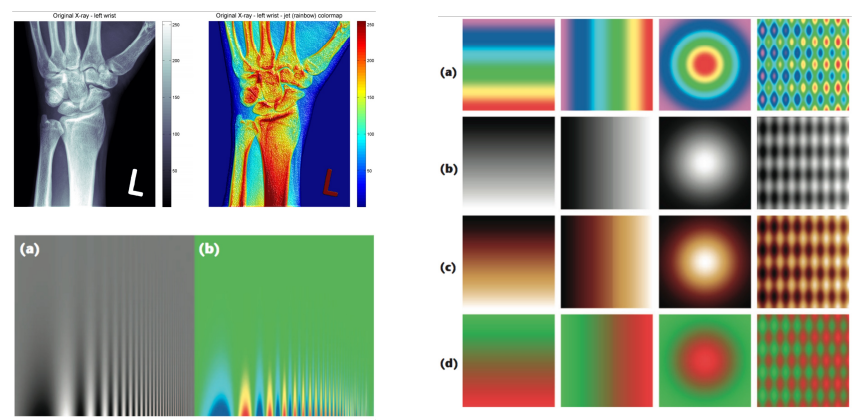
    example

    • sometimes colorless is better
    Use perceptually uniform colormaps

    example

    • except Google Turbo Colormap (Rainbow) is actually perceptually uniform

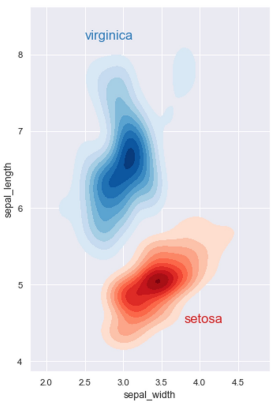
    • use colors to highligh data type example

      • Qualitative: choose qualitative scheme that helps distinguish categories
      • Quantitative: choose color scheme that implies magnitude

    • Sequential and Diverging

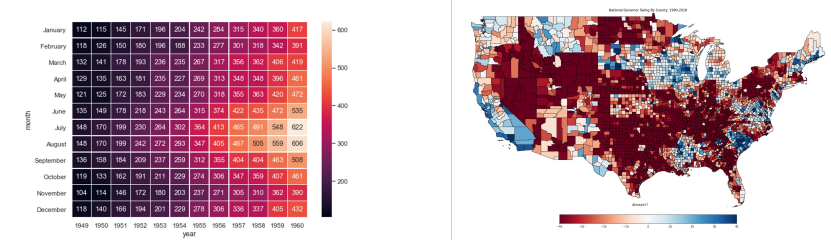
      example

      • left (sequential scheme): light color = extreme values
      • right (diverging scheme): light color = middle (neutral) values

    • good to use color packages

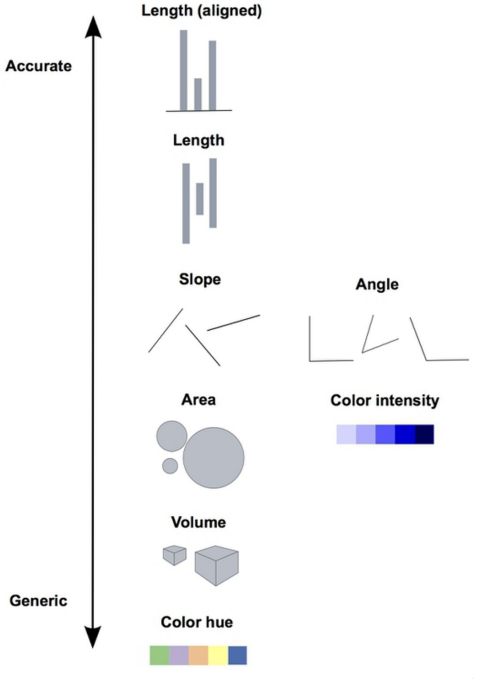
  • Markings example

    • \(\Rightarrow\) accurate preferred
    • Lengths are easy to distinguish (bar graphs)
    • avoid:
      • angles & areas (pie charts)
      • wordclouds
      • jiggling baseline (stacked bar charts, area charts)
    • related: Overplotting

Context

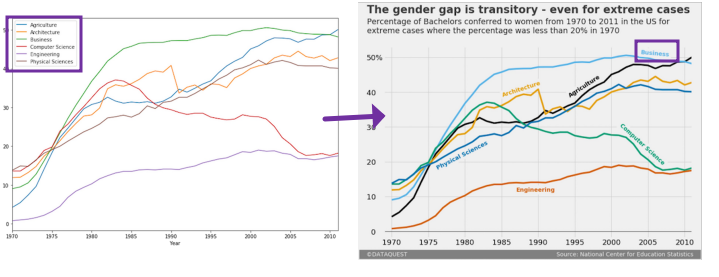
  • instead of keys, better if labeled directly example
  • add context directly to plot
  • captions: comprehensive, conclusions …etc

Smoothing

  • Histograms : smoothed version of rug plots
  • Smoothing

    allows to focus on general structure rather than individual observations

    • points : [ 2.2, 2.8, 3.7, 5.3, 5.7 ]

    • bins : [0,2), [2,4), [4,6), [6, 8]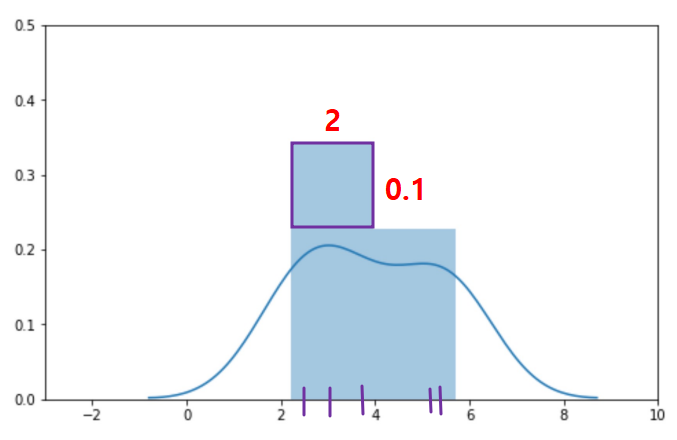 example

    • area = proportion, (2 * 0.1) * 5 = 1

  • KDE : Kernal Density Estimation

    • estimate probability density function (or density curve)
    1. Place kernal at each data point example
    • 1.1: choose \(kernal\) and \(bandwidth (\alpha)\)
      • kernal : Gaussian, alpha = 1
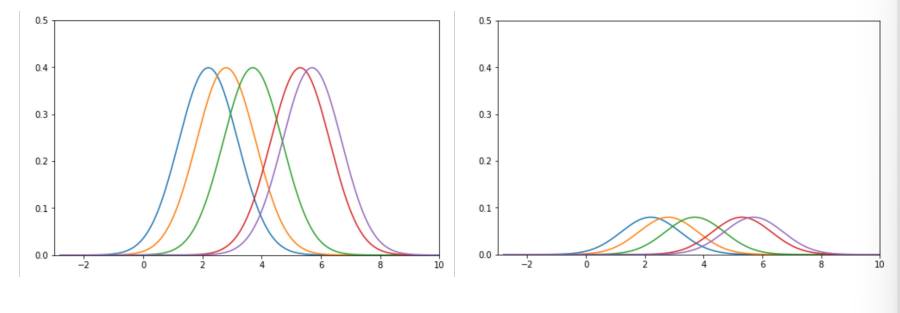
    1. Normalize Kernals example
    • 5 different kernals with area 1 each
    • we want area = 1 altogether \(\Rightarrow\) multiply each by \(1/5\)
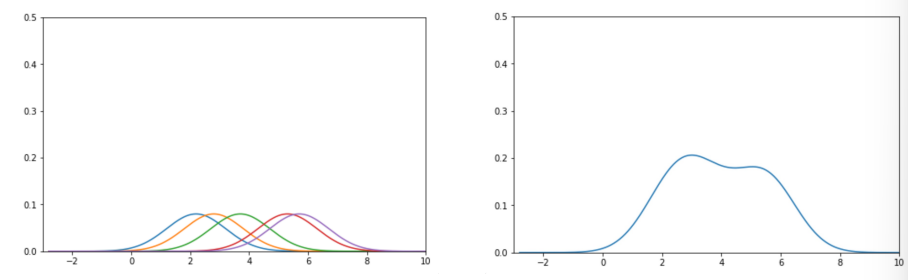
    1. Sum Kernals example
    • kernel density estimate

      = sum of the normalized kernels at each point

    • \(\Rightarrow\) same result as sns.distplot !

  • Kernals: valid density function

    1. must be non-negative for all inputs
    2. must integrate to 1

    • \(Gaussian\): most common kernal \[K_a(x, x_i) = \frac{1}{\sqrt{2\pi\alpha^2}}e^{-\frac{(x-x_i)^2}{2\alpha^2}}\]

      • \(x\) : any input
      • \(x_i\) : \(i^{th}\) observed value
      • kernals cenetered on observed values \(\rightarrow\) mean of distribution = \(x_i\)
      • \(bandwidth parameter = \alpha\) : controls smoothness of KDE
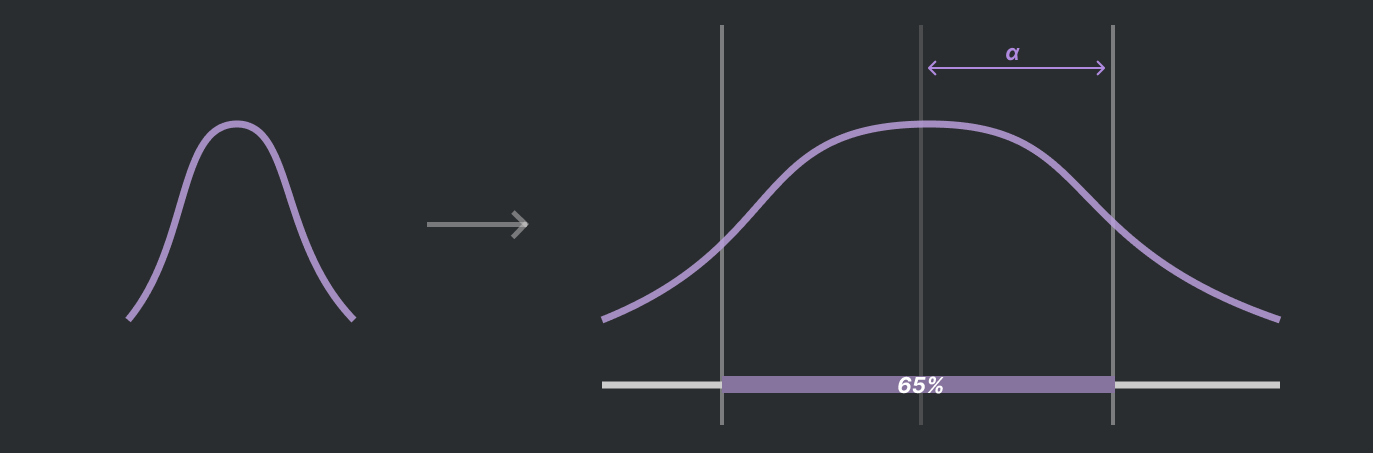
        • also standard deviation of the Gaussian example

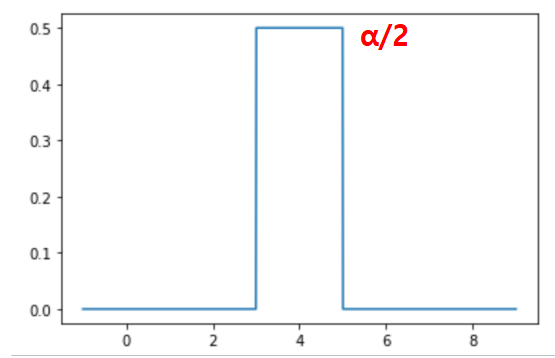
    • \(Boxcar\): another common kernal

      • assign uniform density to points within ‘window’ of observation, 0 elsewehere
      • resembles histogram \(K_a(x, x_i) = \begin{cases} \frac{1}{\alpha}, |x-x_i| <= \frac{a}{2}\\ 0, else \end{cases}\)
        Bocar kernel centered on xi=4 with α = 2

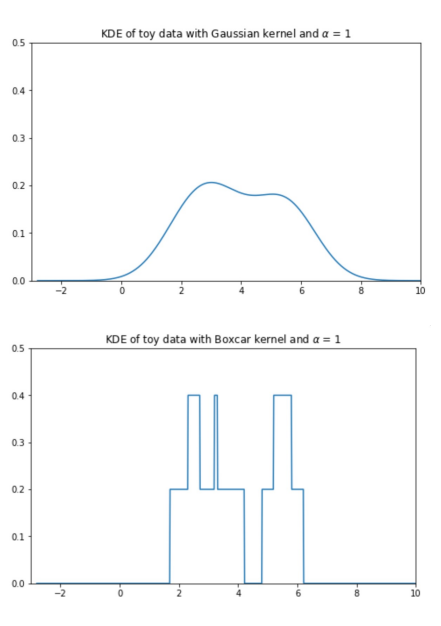
        example </div></details>

        Gaussian vs Boxcar

        example

  • Effect of bandwidth on KDEs

    • bandwidth \(\approx\) bin (in histogram)

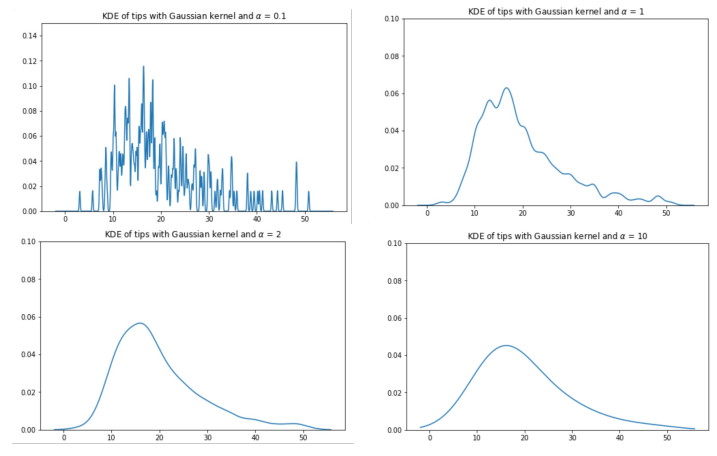
    • KDE becomes smoother as \(\alpha\) increases example

    • simpler to understand, but gets rid of potentially important distributional information
    • \(\alpha\) : hyperparameter
  • Summary of KDE: \(f_\alpha(x) = \frac{1}{n}\sum_{i=1}^{n} K_\alpha(x, x_i)\)
    • \(x\): any number on the number line (input to our function)
    • \(n\): number of observed data points
    • \(x_i (x_1, x_2,...,x_n)\) : observed data point (used to create KDE)
    • \(\alpha\) : bandwidth or smoothing parameter
    • \(K_\alpha(x, x_i)\) : kernal centered on observation \(i\)
      • each kernal individaully has area = 1. We multiply by 1/n so that total area = 1

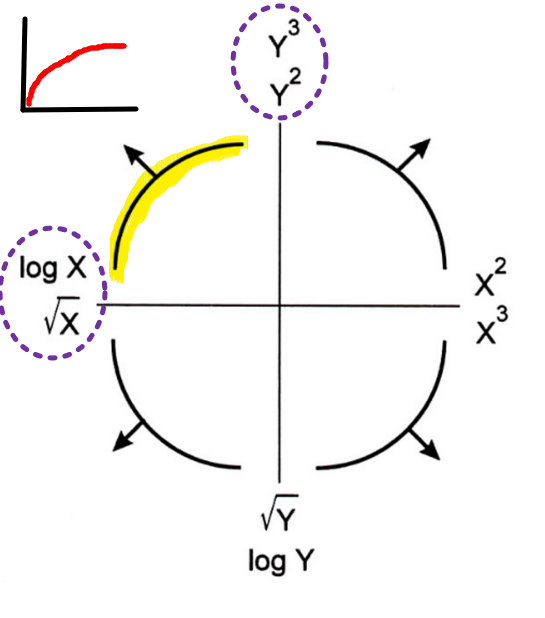
Transformation

  • transforming data can reveal patterns
    • ex: when distribution has large range, log useful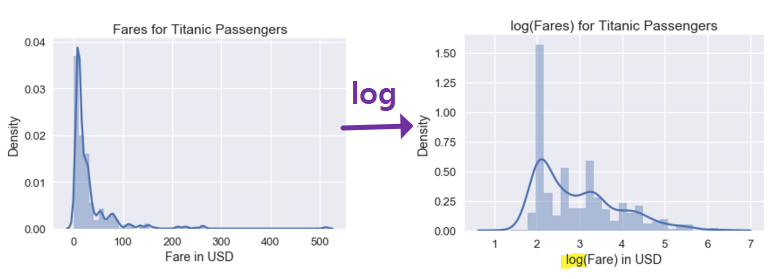 example

  • linearize

    • good because we can automatically known relationship between x and y \(\Rightarrow\) simple to interpret

  • log review

    • \(y = a^x\) \(\rightarrow \log (y) = x\log (a)\)
    • \(y = ax^k\) \(\rightarrow \log (y) = \log (a) + k \log (x)\)
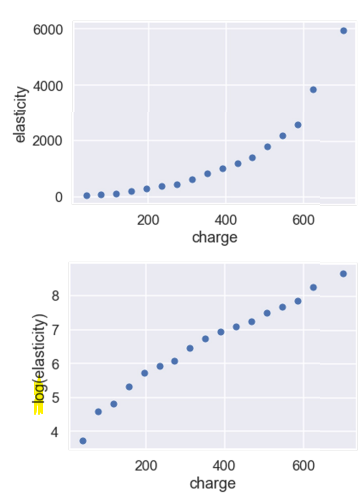
  • Log of y-values
    • \(\log y = ax+b\) \(\rightarrow \log y = ax+b \rightarrow y = e^{ax+b} \rightarrow y = e^{ax}e^b \rightarrow y = Ce^{ax}\)
    • \(\Rightarrow\) exponential relationhip example

  • Log of x and y-values

    • \[\log y = a \cdot \log x+b\] \[\rightarrow \log y = ax+b \rightarrow y = e^{a\cdot \log x+b} \rightarrow y = Ce^{a\cdot \log x} \rightarrow y = Cx^a\]

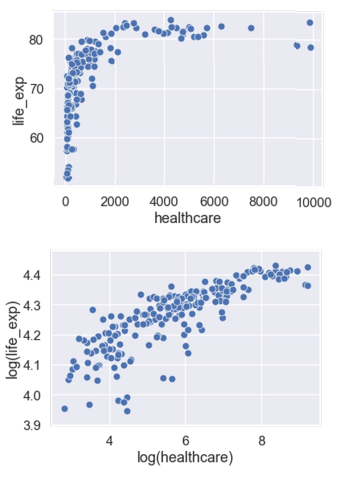
      example

    • \(\Rightarrow\) power relationhip (one-term polynomial)
  • Turkey-Mosteller Bulge Diagram

example

  • following will help linearize
  • multiple solutions exist, some will fit better than the others
  • \(sqrt\) and \(log \rightarrow\) smaller
  • \(power \rightarrow\) bigger
  • these transformations will result in increasing / decreasing scale of axis
Example

example