01 Probability and Data Design

in Notes / Dataanalytics / Datascience

Day 1-2

Data Science Lifecycle

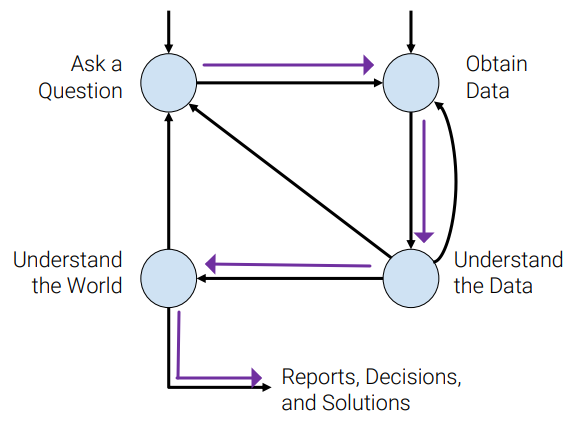
lifecycle

1) Ask a Question (Problem Forumulation)
- What do we **want to know**? 
- What **problems** are we trying to solve?
- What are the **hypotheses** we want to test?
- What are our **metrics** for success?
2) Obtain Data (Data Acquisiton and Cleaning)
- What data do we **have** and what data do we **need**?
- How will we sample **more data**?
- Is our data **representative** of the population we want to study?
3) Understand the Data (Exploratory Data Analysis (EDA) & Visualization) ↕️
- How is our data **organized** and what does it contain?
- Do we already have **relevant data**?
- What are the **biases**, **anomalies**, or other **issues** with the data?
- How do we **transform** the data to enable effective analysis?
- usually the **longest process**for data analysts
4) Understand the World (Prediction and Inference: Machine Learning)
- What does the data say about the world?
- Does it answer our questions or accurately solve the problem?
- How robust are our conclusions and can we trust the predictions?
  • 5) Reports, Decisions, and Solutions

Censuses and Surveys

CensusSurveys
done periodically, usually led by government and for their purposes (collecting all data)set of questions
≈ official count / survey of a population, typically recording various details of individualswhat/how is asked affects answers and whether they will answer or not
  • not all census leads to good respondance rate \(\Rightarrow\) should make good survey questions

Samples

Quality, not qunatity!

  • Census is great, but 1) EXPENSIVE and 2) DIFFICULT TO CONDUCT
  • \(\Rightarrow\) sample : subset of population
    • often for inferences about the population
    • How to draw sample affects accuracy
    • commmon errors
        1. Chace Error (easy, random sampling): random samples can vary from what is expected, in any direction
        1. bias (hard, non-random samples): a systematic error in one direction

Non-Random Sampling

CONVENIENCE SAMPLES

  • whomever/whatever is convenient for investigators
  • bias may occur (unpredictably)
  • should not be used in official docs / papers

lifecycle

  • bias ex) sample ones near the door = mice that are running away
    • \(\Rightarrow\) cannot represent total mice population

QUOTA SAMPLES

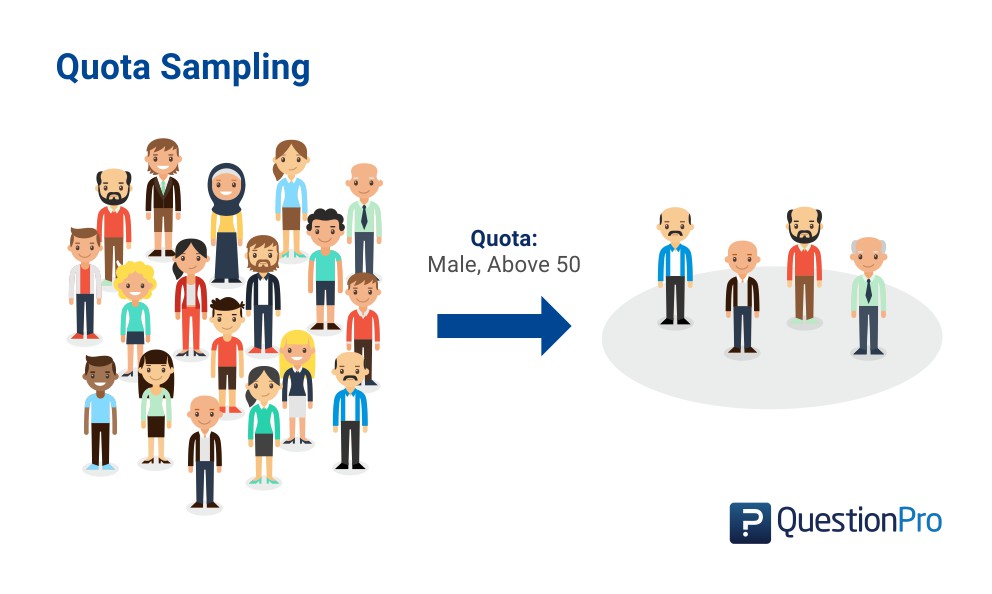
lifecycle

  • restricts selection of sample by controlling the number of respondents by one or more criterion
  • disadvantages: might be tempted to interview those who look helpful
  • biased: not everyone gets ta chance of selection

CASE STUDY Study: 1936 US Presidential Election

  • widely used sample

    Literary Digest:

  • magazine that successfully predicted election outcomes 5 times
  • Franklin Roosevelt \(D\) vs Landon \(R\) => predicted Landon’s election
  • sent out 10,000,000 surveys to individuals found from
    • 1) phone books
    • 2) list of magazine subscribers
    • 3) list of country club members
  • usually the rich people (who used those) went for Landon (\(R\))
  • Sample method was biased
  • Only 2.4 million people actually filled out survey (24% response rate)

    Gallup’s Poll:

  • statistician, also made predictions
  • successfully predicted with only 50,000 surveys
  • knew that Literary Digest would come up with that solutions with that method
    • used the same method only on 3000 people and got the same result
 $Roosevelt#surveyed
Literary Digest Poll43%10,000,000
George Gallup’s Poll56%50,000
Gallup’s prediction of Digest’s prediction44 %3,000
Actual Election61%All voters

\(\Rightarrow\) Big samples aren’t always good, representative matters

  • bias will be magnified with larger sample size

Population, Samples, and Sampling Frame

  • Population : The group that you want to learn sth about
  • Sampling Frame : list from which the sample is drawn.
  • Sample : actual sampling (subset of sampling frame)

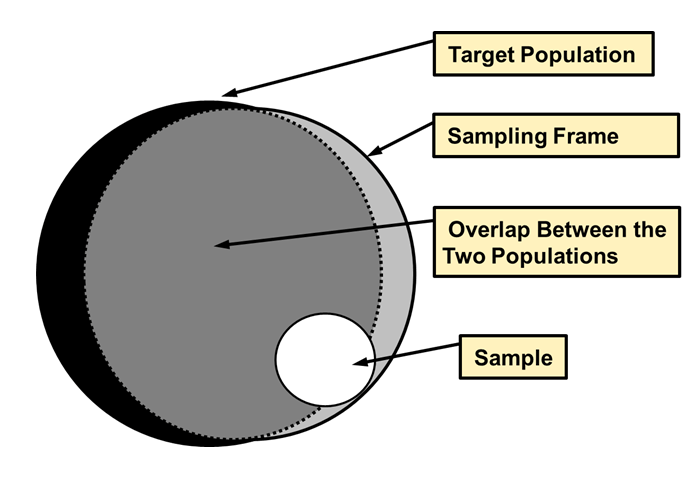
lifecycle

  • sampling frame (and sample) may not contain individuals from population
  • ideal but not easy: \(population === sampling frame\)

Common Biases

  • Selection Bias : systematically excluding/favoring particular groups
    • avoid by examining the sampling frame and method of sampling
  • Reponse Bias : People don’t always response truthfully
    • avoid by examining the nature of questions + method of surveying
  • Non-response Bias
    • people don’t always respond
    • avoid by keeping surveys short & persistent

Probability Samples

  • can assign precise prob. to each event drawn
  • can quantify uncertainty/confidence about an estimator, prediction, or hypothesis test

  • standard errors, p-values, or confidence levels are reported without a proper explanation of the sampling procedure \(\Rightarrow\) determine correctness of sampling

  • must be able to provide chance that any specified set of individuals will be in the sample
  • All individuals in the population do not need to have the same chance of being selected.
  • still be able to measure the errors (since all prob. is known)

Simple Random Sample (SRS)

lifecycle

  • most widely used sampling
  • sample drawn uniformly at random without replacement
    • if sample size small (compared to population) then ≈ random with replacement
  • Number of ways to select an SRS of size \(n\) from population \(N\)
\[\binom{N}{n} = \frac{N!}{n!(N-n)!}\]
  • Chance that a particular element of population is selected by SRS:
\[\frac{\binom{N-1}{n-1}}{\binom{N}{n}}\]
  • MIDTERM

EXAMPLE SCENARIO

  • 1200 students lined up alphabetically
  • 1 of first 10 students picked randomly

  • every 10th student picked after that (ex: 2, 12, 22, …) lifecycle

  • Is this a probability Sample?
    • YES: if sample is [n, n + 10, n + 20, ..., n + 1190] where 0 <= n <= 10, probability of sample = 1/10
    • otherwise, probability is 0
    • only 10 possible samples
  • Does each student have the same probability of being selected?
    • YES: each can be chosen with probability of 1/10
  • Is this a Simple Random Sample?
    • NO : chance of selecting \((8,18)\) = 1/10;
    • chance of selecting \((8,9)\) = 0
  • Common Approximation
    • common situation: enormous population, but only a small number of sample affordable
    • recall that if the population is huge compared to the sample,
      • random sampling with replacement ≈ without replaecment
    • \(\Rightarrow\) Probabilities of sampling with replacement are much easier to compute!

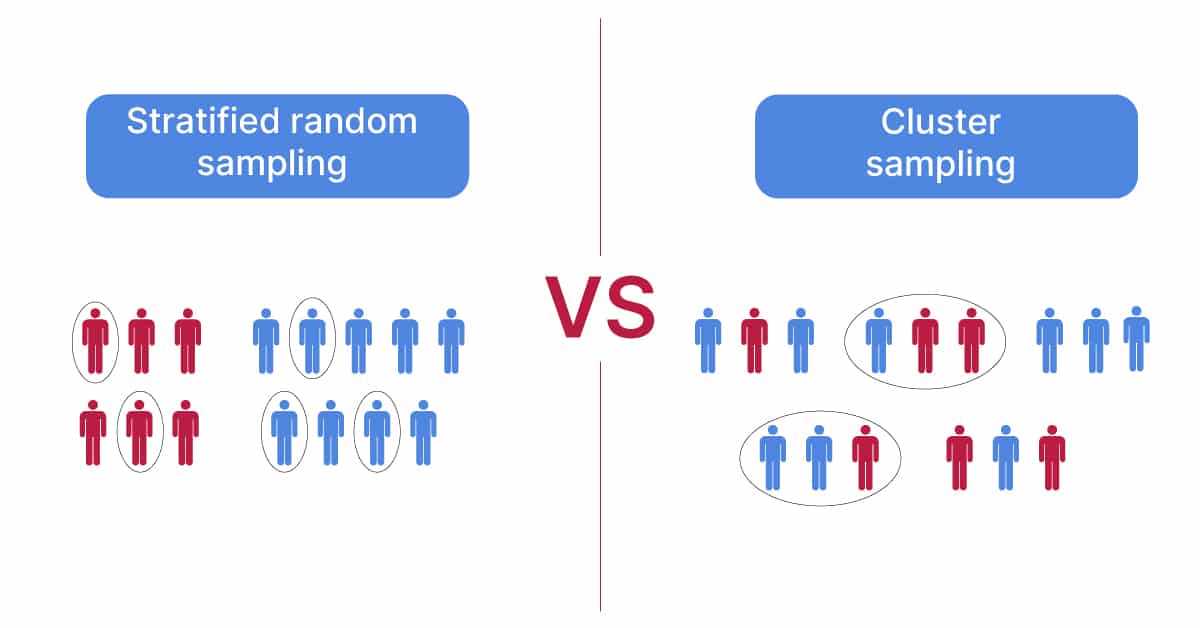
Cluster Sample

  1. The population is divided into clusters of individuals.
  2. One then uses SRS to select entire clusters instead of individuals.
  • makes data collection easier
  • BUT greater variation in estimation \(\Rightarrow\) larger samples than SRS required

Stratified Sample

  1. The population is divided into strata of individuals, e.g., based on demographics.
  2. Select SRS of individuals in each stratum.

CLUSTER vs STRATIFIED

  • lifecycle lifecycle

  • MIDTERM + midterm questions

Designed Experiment

  • divide groups for examination
    • 1) control group
    • 2) investigate group

Randomized controlled trial (RCT)

  • A type of designed experiment in which participants in the trial are randomly allocated to either (one can end up randomly in either control \(\mid \mid\) investigation group)
  • often the gold standard for many types of investigations (ex: clinical trial)

Observational studies

  • Examine the association/effect of a treatment on an outcome when the variable of interest is not under the control of the investigator
    • E.g. Study effect of smoking on health

A/B Testing

lifecycle

  • Determine whether two samples were drawn from the same population, i.e. have the same data generating distribution.
  • widely used for marketing, website/mobile app design
  • (2000) Google engineers ateempted to find out optimal # of results in serach engine