11 Regularization

in Notes / Dataanalytics / Datascience

Introduction

  • Noise: part of \(y\) we cannot model
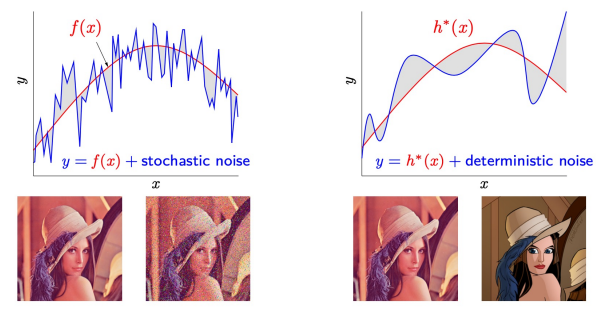
    • noise
    • noises (stoch/deter.) lead to overfitting (learning에 피해줌)
    • Humans: extract simple patterns (ignore \(noise\) and complications)
    • but computers: 모든 픽셀에 대해 같은 기준을 가지고 판단
      • \(\Rightarrow\) we need to simplify for them feature extraction, regularization, attention

Overfitting

  • consequences:
    1. Fitting observation (training error, \(E_{in}\)) no longer indicates decent test error (\(E_{out}\))
      • \(E_{in} \approx E_{out} \leftarrow\)best
    2. \(E_{in}\) no longer good guide for learning

  • observed when:

    • model too complex to represent target (필요 이상으로)
    • model uses its additional DOF (Degree of Freedom) to fit noise in data like increasing number of features (increasing number of w in linear model w^Tx)
    • small # of data \(\rightarrow\) (not enough data) easy to learn model
      • \(\Rightarrow\) few-shot (using only use small number of data) / zero-shot learning
  • overfitting을 잘 다루는 것이 전문가와 아마추어의 차이

Regularization

improving \(\hspace{0.1cm} E\_{out}\)

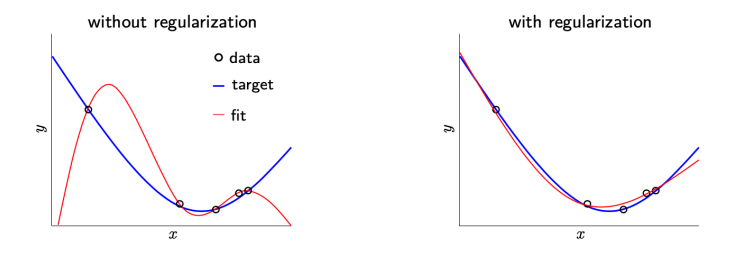
noise

  • overfitting: \(f \neq g \rightarrow\) sample error \(\uparrow\)

  • side effects: may become incapable of fitting \(f\) faithfully

  • Strategies:

    1. put extra constraints (ex: add restrictions on parameter values)
    2. add extra terms in objective function(like soft constraint on parameter values)
    3. combine multiple hypotheses that explain training data(aka ensemble methods)
      • extra constraints/penalties requires Domain knowledge & preference for simpler model

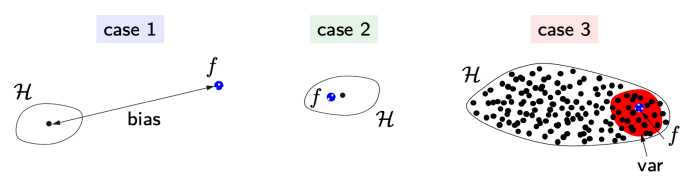
noise

casemodelmain errorphenomenon
1exclude \(f\)biasunderfitting
2match \(f\)  
3include \(f\) but many othersvarianceoverfitting
  • GOAL: case #3 \(\Rightarrow\) case #2

Theory of Regularization

  • Regularization: process of introducing additional information to solve problem or overfitting (restrictions for smoothness or bounds on vector space norm)

  • example: \(z= \theta _0 + \theta _1x_1 + \theta _2x_2 + \theta _3x_3 + \theta _4x_4 + \cdots + \theta _{5000} x_{5000}\)
    • too many features \(\rightarrow\) remove some by making \(\theta\) into zero

  • Approaches:

    1. Mathematical: function approximation
    2. Hueristic: handicapping minimization of \(E_{train}\)

  • Generalization bound Review:

    • \(f\): unknown target function (objective of learning)
    • \(g\): our (best) model learned from data (one of \(h\subset \mathcal{H}\))
    • \(\mathcal{H}\) : hypothesis set from which we choose \(g\)
      Hypothesis Set

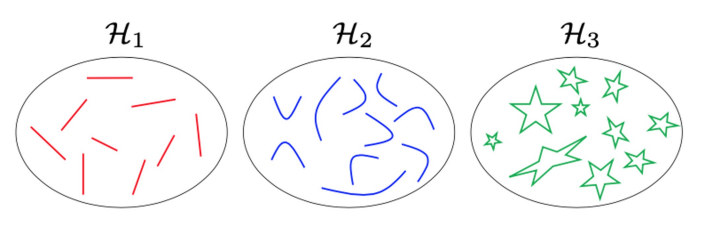
      nestrov

  • VC generalization bound (외울 필요X)

nestrov

  • (3 variables) \(N\): # of examples, \(d_{VC} \approx\) complexity of model

  • \(\Rightarrow E_{out}(h) \leq E_{in}(f) +\) \(\Omega(\mathcal{H})\) for all \(h\in \mathcal{H}\)

    • \(E_{out}\) bounded by penalty \(\Omega(\mathcal{H})\) on model complexity
  • VC BOUND: \(E_{test}(h) \leq E_{train}(f) + \Omega(\mathcal{H})\) for all \(h\in \mathcal{H}\)
    • \(\Rightarrow\) GOOD, can fit data using simple \(\mathcal{H}\)
  • REGULARIZATION: even better, can fit using simple \(h\in \mathcal{H}\)
    • find \(\Omega(h)\) for each \(h\)
    • minimize BOTH \(E_{in}(h)\) and \(\Omega(h)\) (원래: \(E_{in}(h)\)만 minimize 했었음)
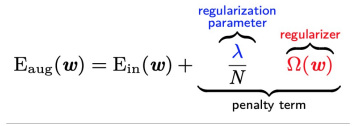
    • nestrov
    • \(\Rightarrow \Omega(\mathcal{h})\)도 이제는 최적화해야할 부분 \(\rightarrow\) avoid overfitting by constraining learning process!
    • \(N\) 이 커질수록 regularization 필요없어짐 \(\rightarrow \frac{1}{N}\) 빼버리기 \(\Rightarrow\) optimal \(\lambda\) less sensitive to \(N\)

    • ex: Weight Decay Regularizer : minimize \(E_{train}(w)+\) \(\frac{\lambda}{N}w^Tw\) one more term added

    • A member of even a large model family can be appropriately regularized
  • How to select \(\Omega\) and \(\lambda\)
    • regularizer \(\Omega \leftarrow\) heuristic (주로 data보기도 전에 fixed)
    • parameter \(\lambda \leftarrow\) principled :
      • 주로 depends on data
      • overdose \(\Rightarrow\) underfitting (validation이 알려줄 것임)

      overdose

Regularization Techniques

1. Norm Penalties

  • \(midterm\) : PROS & CONS of these

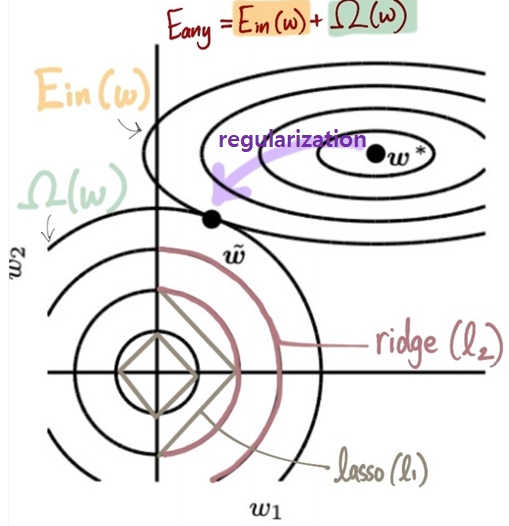
  • most famous: \(l_1\) and \(l_2\) regularizers
  • Lasso - \(l_1\) regularizer
    • convex but not differentiable everywhere
    • variable shrinking + selection \(\Rightarrow\) sparse solution
    • \[\Omega(w)= \parallel w \parallel _1 = \sum _q \mid w_1 \mid\]
    • problem: \(\mid w_q \mid \rightarrow V\) shaped, not differentiable at some point
  • Ridge (statistics) - \(l_2\) regularizer
    • math friendly (convex / differentiable)
    • no sparse solution
    • variable shrinking only (shrink \(w\)’s of correlated \(x\)’s)
    • \[\Omega(w)= \parallel w \parallel _2 = w^Tw = \sum _q w^2_q\]
      • \(E_{aug}(w) \hspace{1cm}=\) \(E_{in}(w)+\frac{\lambda}{N}\Omega(w) \hspace{1cm}= E_{in}(w)+\frac{\lambda}{N}\) \(w^2\)
      • goal: minimize \(E_{aug}\), but \(w\) can be further minimized if \(\lambda\) (parameter) gets increased
      • if \(w\) gets minimized, then more likely features disapper (w=0) \(\rightarrow\) increase linearity (regularize and reduce overfitting)
  • weight decay meaning
    • \(w \leftarrow\) \(w-\epsilon \nabla E_{aug}(w)\)
      \(E_{aug}(w)= E_{in}(w)+(\frac{\lambda}{N}\Omega(w))\)
    • \(\hspace{0.1cm} =\) \(w-\epsilon \nabla E_{train}(w) -2\epsilon \frac{\lambda}{N} w\)
    • \(\hspace{0.1cm} =\) \((1-2\epsilon \frac{\lambda}{N})\)\(w-\epsilon \nabla E_{train}(w)\)
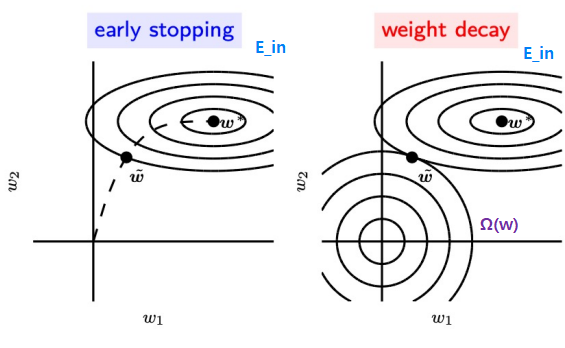
  • another analysis of weight decay
    • weightdecay
    • rescale \(w^*\) along the axes defined by eigenvector of \(H \Rightarrow \widetilde w\): optimized \(w\)
    • Scale factor for ith eigenvector: \(\frac{eigenvalue(H)_i}{eigenvalue(H)_i + \lambda}\)
    • \(w_1\) direction (\(\leftrightarrow\)): eigenvalue \((H)_1\) small \(\rightarrow\) no strong preference
    • \(w_2\) direction (\(\updownarrow\)): eigenvalue \((H)_2\) large \(\rightarrow\) affects this direction a little
  • Tkhonov Regularizer
    • Generalization of weight decay (make \(\alpha \neq 1\leftarrow\) not sure)
    • \(\Omega(w) =\) \(w^T\Gamma ^T \Gamma w = \sum _p \sum _q w_pw_q\gamma _p \gamma _q\)
  • Elastic-net penalty
    • lasso (\(\alpha = 1\) ) + ridge (\(\alpha = 0\) )
    • \[\Omega(w) = \sum _q {\alpha \mid w_q \mid + \frac{1}{2}(1-\alpha) w^2_q}\]
  • Comparisons
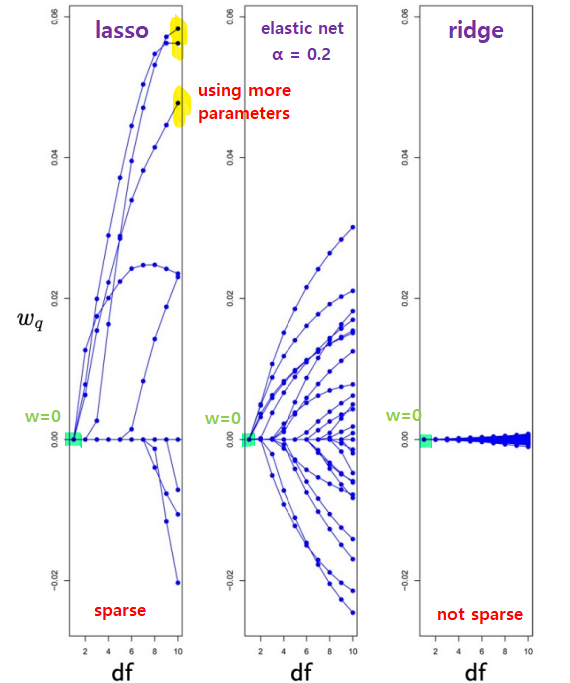
    • parameters
    • DF: Degree of freedom (클수록 can use many parameters)
    • \(\lambda\) \(\Omega(w)\)
      • \(\lambda\) 클수록 not used by \(w\) (\(w=0\))
      • 낮으면 \(w\)가 parameter ( \(\lambda\) )사용할 것 ????

2. Early Stopping

  • overfitting: \(E_{in} \searrow\) but \(E_{val} \nearrow \longrightarrow E_{val}\)이 낮아지면 멈춰버리면 어떨지?
  • Early Stopping

    : keep track of both \(E_{in}\) and \(E_{val}\)

    • parameters
    • stop training with lowest \(E_{val} \Rightarrow\) potentially better \(E_{out}\)
    • effective/simple \(\rightarrow\) popular in machine learning
  1. Every time error on validation set improves
    • store copy of parameters (returned when terminated)
  2. Algorithm terminate when no improvement in \(E_{val}\)
  • Advantages:
    • unnoticeable (weight decay: \(E_{in}-\Omega(w)\) 중 \(\Omega(w)\) 가 없는 셈)
    • Early Stop \(\Rightarrow\) fewer epochs \(\Rightarrow\) computational savings
    • leave extra data for additional training
  • Disadvantages:
    • 주기적으로 \(E_{val}\) compute 해줘야 함 (validation error이 많으면 inefficient) \(\Rightarrow\) seperate GPU, small val set, infrequent validation = 해결책
    • additional memory to store best parameters (근데 거의 신경 X)
  • Early Stopping vs Weight Decay
    • parameters
    Early StoppingWeight Decay
    minimize \(E_{in}\) onlyminimizes both \(E_{in}\) and \(\Omega (w)\)
    monitors \(E_{va}\) to stop \(\Rightarrow\) auto-determines correct amount of regularizationrequires many training experiments with different hyperparameters

3. Ensemble Methods

make strong model by combining weak models

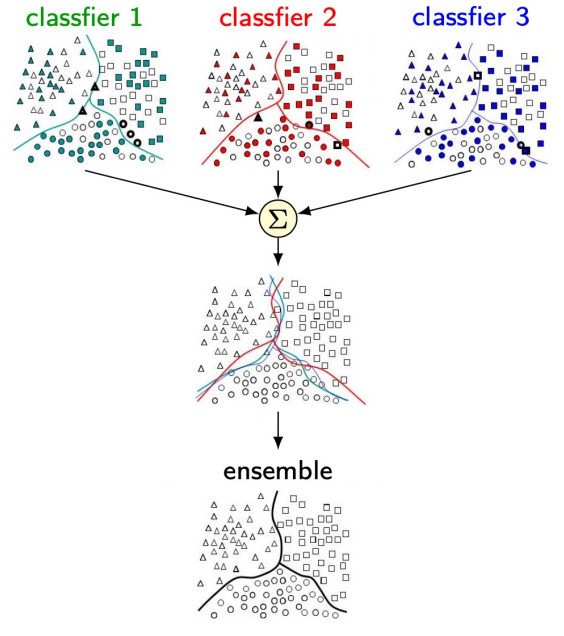
parameters

  • aka ‘model averaging’
  • strong: better bias/variance/accuracy
    • variables
  • Assumption:
    • (i) Different models \(\rightarrow\) different random mistakes
    • (ii) Averaging Noise \(\rightarrow\) 0
  1. (weighted) voting
  2. Bagging
    • bootstrap aggregating 의 약자
    • improve model’s variance but not bias
    • bagging
    • train seperately \(\Longrightarrow\) combine outputs by averaging
    • make \(k\) different datasets (random sampling)
    • reduce same model/training algo/obj function \(\Rightarrow\) training different models
  3. Boosting
  • constructs an ensemble with higher capacity than individual models
    • meta-algo for primarily reducing bias & variance
    • most famous: AdaBoost
  • train multiple weak learners sequentially to get stronger learner
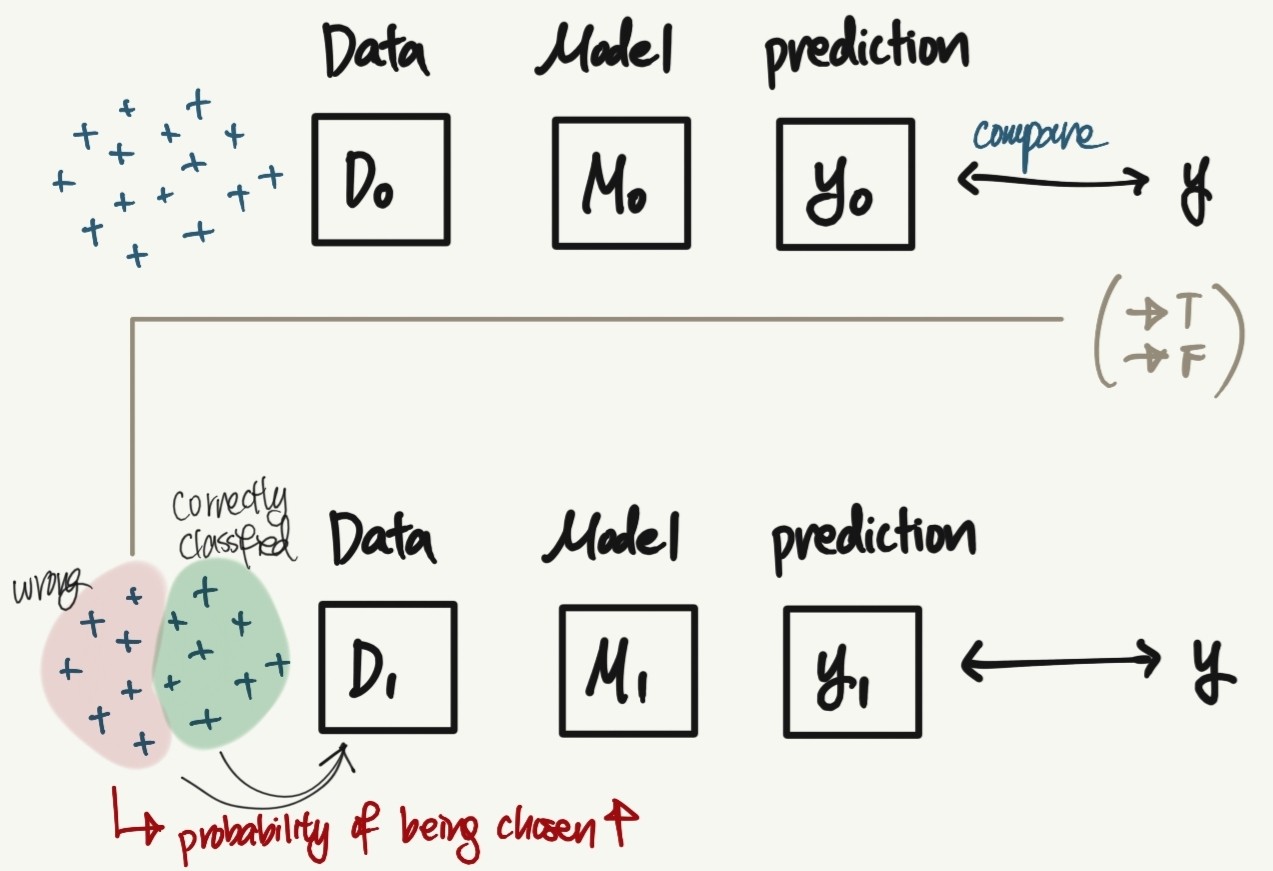
    • boosting
    • future learners: 잘못 분류한 데이터에 더 집중함 (by reweighting training examples with prev learning results)
  • boosting in NN:
    • incrementally add Neural Nets to the ensemble
    • incrementally add hidden units to Neural Nets

parameters

  • model ensembles: extremely powerful, famous, widely used in papers, ML contests …etc
  • typically gives about 2% extra performance

    Questions

  • sparse solution이 뭐냐 (l_1 regularizer)
  • l1 l2 pro cons 정리하기
  • eigenvalue 부분 … in weight decay
  • lambda 클수록 omega 사용 불가? 이거 뭐지