13 Clustering

08 Jun 2023 in Notes / Dataanalytics / Datascience

Review: Taxonomy of ML

Supervised Learning (Labeled Data)
- Regression : Quantitative Response still mostly used for classification...
- Classification : Categorical Response
Unsupervised Learning
(Unlabeled Data)
- Dimensionality Reduction
- Clustering
- example: Netflix, Reverse Engineering Biology

pick arbitrary \(k\), randomly place \(k\) “centers”, each a different color
repeat until convergence:
- color points according to the closest center
- move center for each color to center of points with that color

kmeans

iteration 4 and 5: Centers moved slightly (no points changed color)
iteration 5 and 6 (not shown): no change \(\Rightarrow\) END
[참고] K-Means \(\neq\) K-Nearest Neighbors
- K-Means: Clustering (assigns each point to one of \(K\) clusters)
- K-Nearest Neighbors: Classification (or Regression)

K-Means Clustering for \(K=4\) : each run different output
Need Loss Function to determine BEST
Intracluster Distance (distance within a cluster) \(<\) Intercluster Distance (distance between other clusters)
Loss Functions:

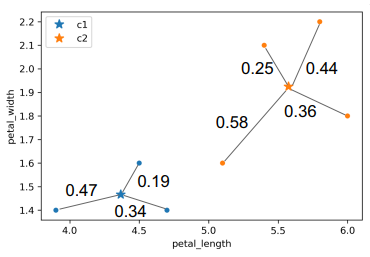
kmeans

Inertia
: Sum of squared distance from each data point to its center
- \(0.47^2 + 0.19^2+0.34^2 + 0.25^2 + 0.58^2 + 0.36^2 + 0.44^2\) \(\)
- lower the better
Distortion
: weighted Inertia
- \(\frac{0.472 + 0.192 + 0.342}{3} + \frac{0.252 + 0.582 + 0.362 + 0.442}{4}\) \(\)

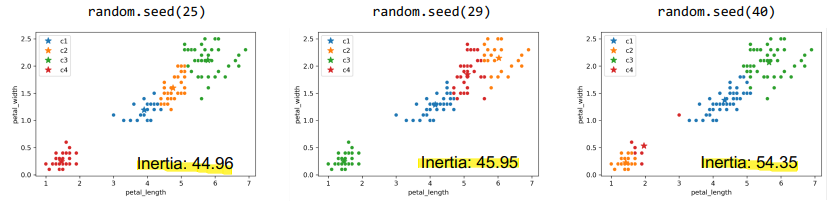
inertia

\(\Rightarrow\) Leftmost (44.96): BEST, Rightmost (54.35): WORST
K-Means try to minimize inertia but often fails to find global optimum
- K Means: 2개의 optimizer이 번갈아가면서 수행한다고 생각하면 됨
  1. First optimizer \(\rightarrow\) center position: hold, data colors: \(optimize\)
  2. Second optimizer \(\rightarrow\) center position: \(optimize\), data colors:hold
- \(\Rightarrow\) neither gets total control: why we iterate
best algorithm so far:
- for all possible \(k^n\) coloring:
  - compute \(k\) centers for coloring
  - compute inertia for \(k\) centers
    - if current_inertia better than best_known:
      - best_known \(\leftarrow\) current_inertia
\(\Rightarrow\) 안쓰는 이유: \(k^n\) too big to compute
inertia will only show local instead of global
no better algorithm found K-Means = NP-hard

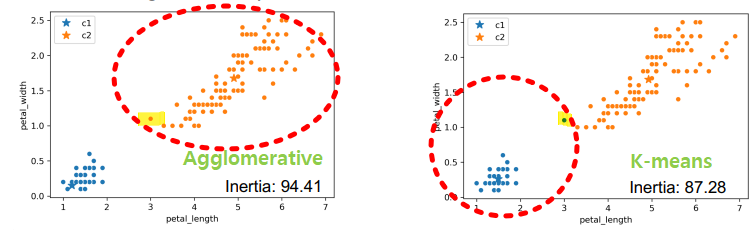
nestrov

K-Means: minimize inertia
- result not guaranteed to optimize inertia
- global optimum 마저 직관적이지 않을 수 있음
Aggolomerative Clustering:
- every data point starts out as its own cluster
- Join clusters with neighbors until \(K\) cluster remains
Example: \(K=2\)

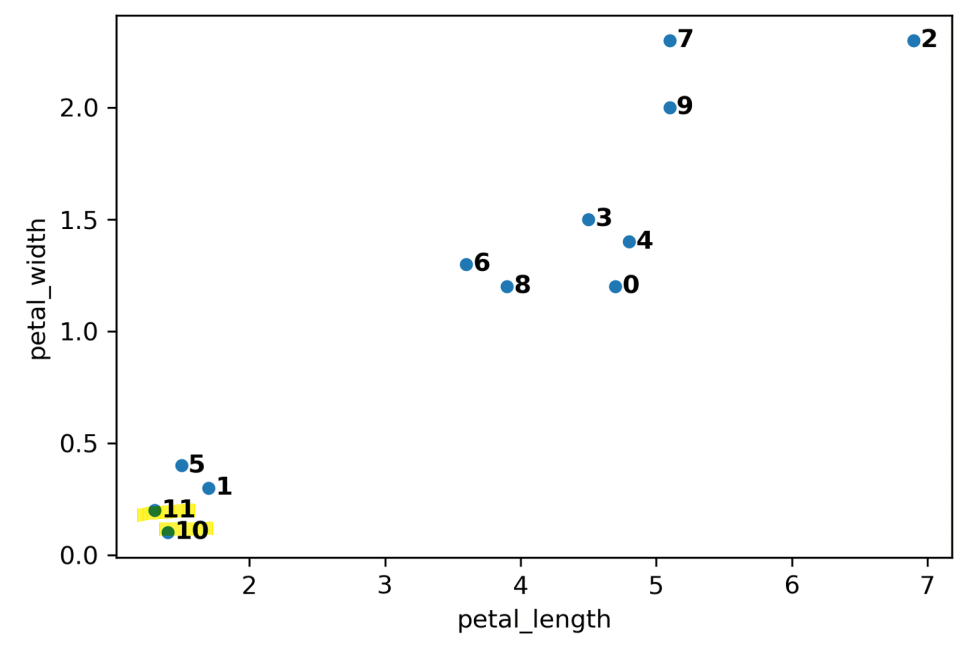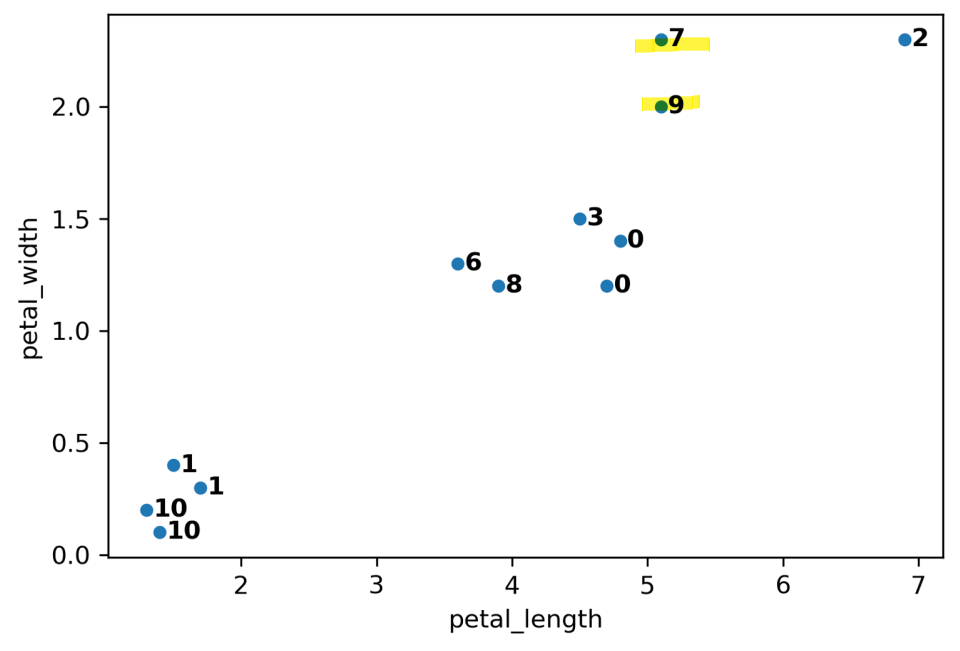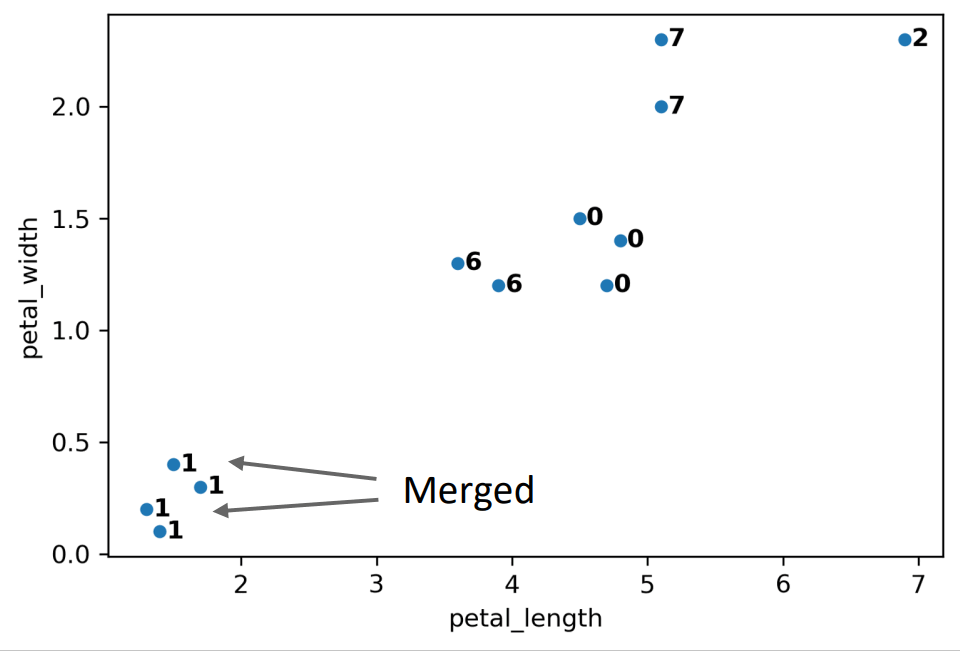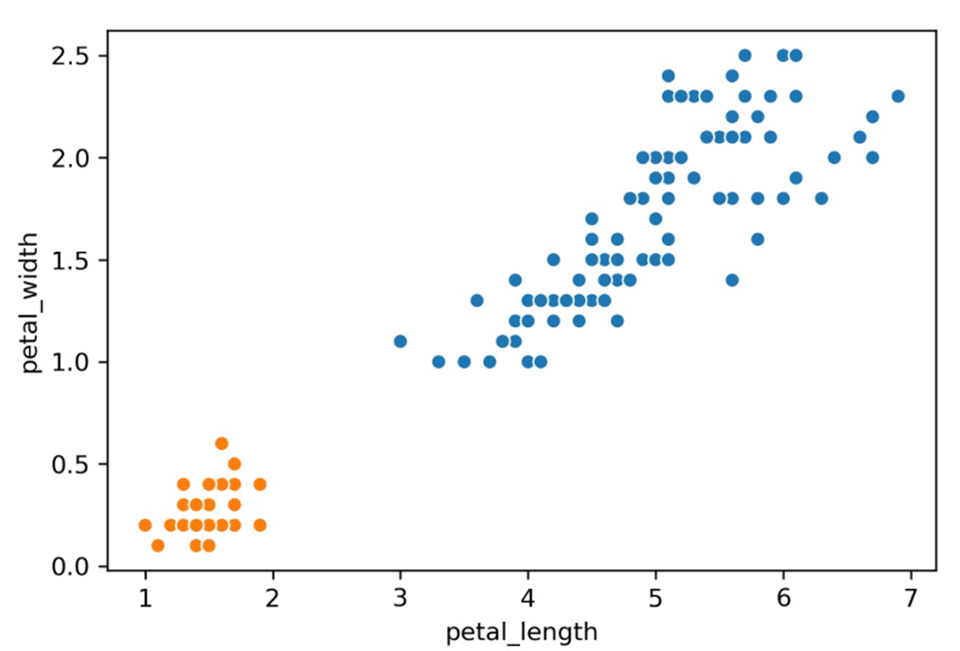
nestrov

note: x-axis & y-axis scale different
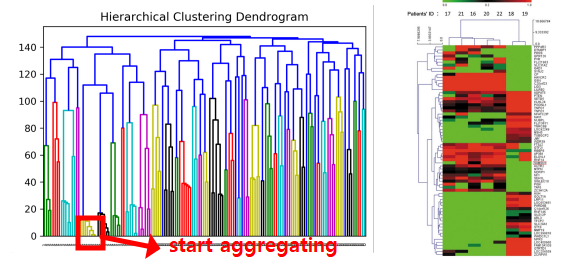
common choice when comparing distances \(\Rightarrow\) max distance
Why it’s also called hierarchical clustering:
- able to keep track of merge (each cluster=tree)
- dendrogram: (\(K=2\))
More clustering Algorithms

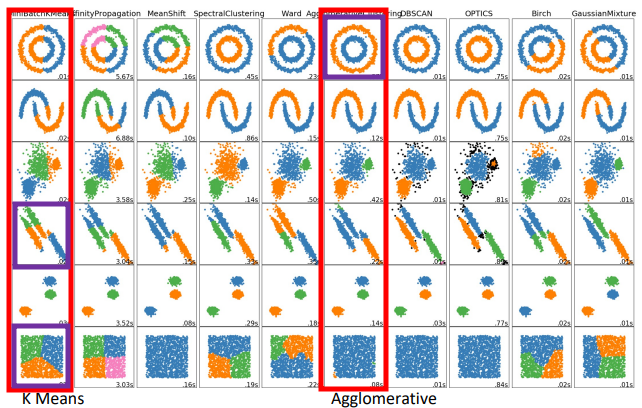
others

Intuitively
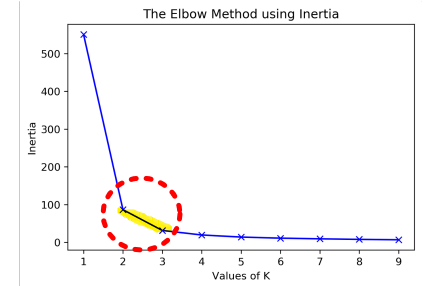
PICK: Elbow Method
- plot inertia versus many different \(K\) values
- pick \(K\) in elbow (하지만 데이터가 복잡하면 elbow없는 경우 다수)
EVALUATE: Silhouette Scores
- check how “well clustered”
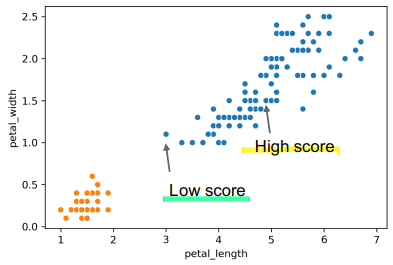
- High Score: near the other points in X’s cluster
- Low Score: Far from other points in cluster
- for data point \(X\), score \(S\):
- \(A\): avg distance to other points in cluster (intra)
- \(B\): avg distance to points in closest cluster (inter)
- \(S=\frac{B-A}{max(A,B)}\) - Observations:
- highest possible \(S\) = 1 (all points in \(X\)’s cluster on top of \(X\))
- \(S\) can be negative when \(X\)’s avg distance within cluster \(>\) avg distance to nearby cluster (\(A > B\))
  - ex: Low Score on graph has \(S=-0.13\)
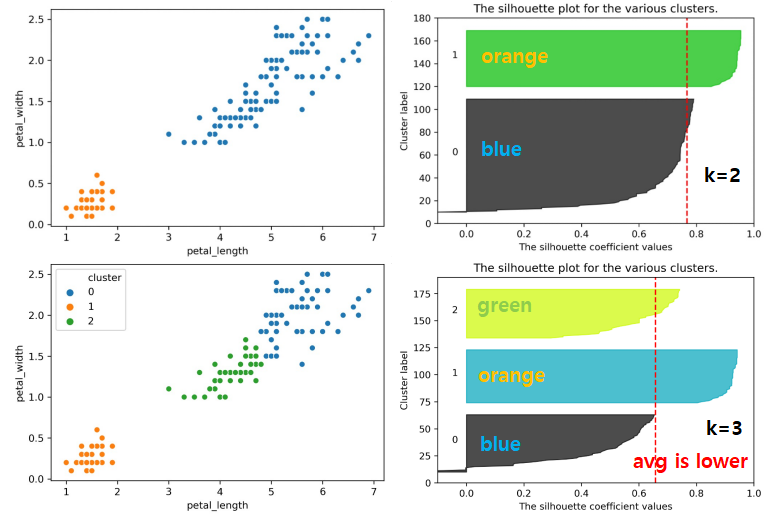
- - points with large silhouette widths = deeply inside cluster
Real World Metrics
- Perform 2 clusterings, for example:
1. cluster heights & weights of customers with \(K=3\) to design [ S, M, L ] t-shirts
2. cluster heights & weights of customers with \(K=5\) to design [ XS, S, M, L, XL ] shirts