Binary Classification

28 Dec 2022 in Notes / Artificialintelligence / Introductiontoai

DAY 3

• Binary Classification
• Binary Classification Basic Idea
  • Binary Classification Steps
  • Linear Regression vs. BC
  • BC Cost Function
• PyTorch implementation🔥

Binary Classification

Classify All Inputs into 0 or 1 (T / F)

Examples & Usages

• Spam Detection: Spam [1] or Ham [0]
• Facebook Feed: Show [1] or Hide [0]
• Credit Card Fraudulent Transaction Detetion: Fraud [1] or Legitimate [0]
  • (determine transaction requested card is stolen or not)
• Tumor Image Detection in Radiology: Malignant [1] or Benigh [0]
  • (determine whether certain cell is harmful or not)

• threshold (한계점)
  • Ex) Quiz_grade > 50 ? PASS : FAIL
  • thresholds can change (if total = 1000, threshold = 50, if total = 10, threshold = 5)
  • ➜ FIX THIS VALUE

Binary Classification Basic Idea

(Review) Deep Learning Steps

1. Make Model
2. Make Cost Function
3. Optimize

Binary Classification Steps

• Step 1: Linear Regression with \(H(X) = WX + b\)
• Step 2: Logistic/sigmoid function \(sig(t)\) based on result of Step 1

TMI: it is called logistic in STATs, sigmoid in CS/EE area

Linear Regression Model	\(+\) Sigmoid Function	➜ Binary Classification Model
Wx + b	sigmoid (z)	sigmoid( Wx + b)
\(H(x) = Wx + b\) or \(H(X) = W^TX\)	\(g(z) = \frac {1}{1+e^{-z}}\)	\(g(X) = \frac {1}{1 + e^{-W^TX}}\)

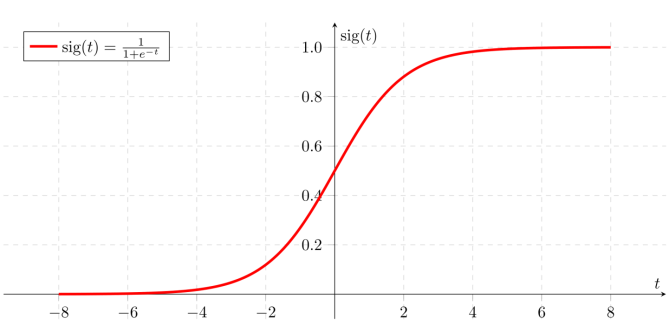
• any inputs (ranging from \(-\infty\) from \(+\infty\) can yield a \(y\) (result) value )

Linear Regression vs. BC

	Linear Regression Model	Binary Classification Model
model	LINEAR	sigmoid(Wx + b)
cost	CONVEX ➜ GDM possible	\(avg( (model-y)^2 )\) ➜ GDM impossible

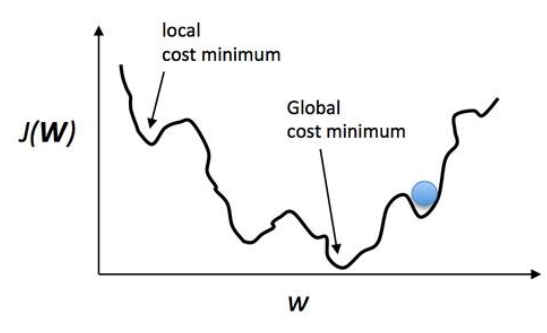
• if unlucky, global cost minimum cannot be achieved ➜ NEW COST FORMULA REQUIRED

  TMI: CONVEX = ∪ shaped

BC Cost Function

\[Cost(W) = \frac {1} {m} \sum \quad c(\quad H(x), \quad y\quad)\]

written into: \[c(\quad H(x), y\quad) = \begin{cases} -log(\quad H(x)\quad) & y = 1 \\ -log(\quad 1 - H(x)\quad ) & y = 0 \end{cases}\]

• Understanding the Cost Function

	Cases:	A	B	C	D
AI model	\(H(X)\)	0	0	1	1	ex ) AI determines correct user is using the credit card
real data	\(y\)	0	1	0	1	ex ) credit card is correctly used by ‘me’ (user)
COST	\(Cost(W)\)	0	\(\infty\)	\(\infty\)	0

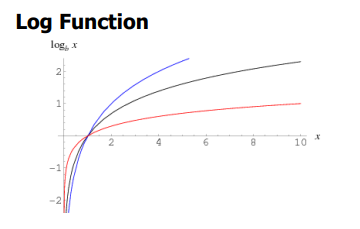
• if AI is correct (CASE A, D) ➜ no Cost
• else COST exists (either stealer uses my card (CASE B) or card suspened (CASE C))

log( 0 ) = \(-\infty\) ; log( 1 ) = 0

Further Explanations

• Case A: my card is not stolen and AI says its not stolen ➜ NO COST
  • \(y = 0\) ➜ \(-log(1 - H(x))\) ⇒ -log ( 1 - 0 ) = -log( 1 ) = 0 (no cost)
• Case B: my card is stolen BUT AI says its not stolen ➜ COST : stealer uses my card
  • \(y = 1\) ➜ \(-log( H(x))\) ⇒ -log ( 0 ) = -log( 0 ) = \(-\infty\) (COST)
• Case C: my card is not stolen BUT AI says it’s stolen ➜ COST : I need to use but my card gets suspended
  • \(y = 0\) ➜ \(-log(1 - H(x))\) ⇒ -log ( 1 - 1 ) = -log( 0 ) = \(-\infty\) (COST)
• Case D: my card is stolen and AI says it’s stolen ➜ NO COST : Denies stealer’s transaction
  • \(y = 1\) ➜ \(-log( H(x))\) ⇒ -log ( 1 ) = -log( 1 ) = 0 (no cost)

• NEW COST FUNCTION (log-based) can derive CONVEX shape ➜ Gradient Descent Possible

• ONE LINE EQUATION (since current Cost function is conditional)

\[c(H(x), y) = \quad -y*\quad log(H(x))\quad -\quad(1-y)*\quad log(1-H(x))\]

• by multiplying \(y\) and \((1-y)\) on both equations and merging them, either one side gets elliminated

\[Cost(W) = -\frac {1}{m} \sum ylog(H(x)) + (1-y) log(1-H(x))\]

➜ Gradient Descent ( \(W \leftarrow W - \alpha \frac{\partial}{\partial W}\) ) Possible

PyTorch implementation🔥

import torch
import numpy as np

# Training Data (nonlinear)
x_train = torch.FloatTensor([[1,2], [2,3], [3,4], [4,4], [5,3], [6,2]]) 
y_train = torch.FloatTensor([[0], [0], [0], [1], [1], [1]]) # 0 or 1 (binary classification)

W = torch.randn([2,1], requires_grad=True) 
b = torch.randn([1], requires_grad = True) 
optimizer = torch.optim.SGD([W, b], lr = 0.01) 

def model_BinaryClassification(x):
  return torch.sigmoid(torch.matmul(x, W) + b)

for step in range(2000):
  prediction = model_BinaryClassification(x_train)
  
  cost = torch.mean( (-1) * ((y_train*torch.log(prediction) + (1-y_train)*torch.log(1-prediction))))
  #BC Cost Function: 1/m * -1 * y       log      H(x)           (1 - y)     log        1 - H(x)
  optimizer.zero_grad() # 0까지 optimize
  cost.backward()       
  optimizer.step()

x_test = torch.FloatTensor([[5,5]]) #예상 답: 1 (PASS)가 나와야 함
model_test = model_BinaryClassification(x_test)
print("Model with [6,1] expectation: 1) in sigmoid: ", model_test.detach().item())

#0.5보다 높은지 안 높은지 실수형 (1.0, 0.0) 으로 변환
model_test_binary = np.round(model_test>0.5).type(torch.float32)  
print("Model with [6,1] expectation: 1) in np.round: ", model_test_binary.detach().item())