07 Learning Problem

in Notes / Dataanalytics / Datascience

Introduction

  • The big picture of Machine Learning (Learning from Data) lifecycle

Problem Setup

  • Formalization:

    • \(X = ℝ^d\) : input space
      • \(ℝ^d\): d-dimensional Euclidean space
      • input vector \(x ∈ X : x = (x_1, x_2, ..., x_d)\)
    • let \(y={+1, -1}\) : output space (\(\rightarrow\) binary decision)

  • Example: credit approval (P/F) of applicants of bank loan

    componentsymbolcredit approval metaphor
    input\(x\)customer application
    output\(y\)approve / deny
    target function\(f : X \rightarrow Y\)ideal credit approval formula
    data\((x_1, y_1), ..., (x_N, y_N)\)historical records
    hypothesis\(g: X \rightarrow Y\)formula to be used
    • \(f\): unkown target function
    • \(X\): input space (set of all possible inputs \(x\))
    • \(Y\): output space (set of all possible outputs)
    • \(N\): the number of input-output examples ( training examples )

    • \(D≜ {(x_1, y_1), ..., (x_N, y_N)}\): data set where \(y_n = f(x_n)\)

    • find \(g(x) \approx y=f(x)\)
    • Example:
      • \(x = \begin{bmatrix} x_1\\x_2\end{bmatrix}\) where \(x_1\): age and \(x_2\): annual salary (in USD)
      • \(N=\) 11, \(d=\) 2, \(X= ℝ^2\), and \(Y=\) { approve, deny}
      • data set \(D\): lifecycle
      • \(\Rightarrow\) linear model (easy, but might not be accurate) \(\rightarrow\) find \(g\) close to \(f\)

  • Learning Algorithms \(A\):

    • use \(D\) to pick a formula \(g : X \rightarrow Y\) that approximates \(f\)
    • choose \(g\) from set of candidate formula under consideration, which we call hyothesis set \(H\)
      • ex) \(H\) = set of all linear formulas \(\rightarrow\) choose best linear fit to \(D\) from this
    • Scenario Example: new customer applies for credit \(\rightarrow\) bank makes decision
      • based on learned \(g\), not on \(f\) (unknown)
      • if \(g\) faithfully replicates \(f\) \(\rightarrow\) decision is reasonable (good)
      Visualized

      example

A simple Learning Model

  • Solution Components
    • give a specific learning problem
      • target function \(f\) (unknown)
      • training examples
      • learning algorithm, hypothesis set
    • Learning Model = \(Learning\) \(Algorithm\) + \(Hypothesis\) \(Set\)
  • Hypothesis Set \(H\):
    • \(H\) specified through \(h(x)\) (\(h ∈ H\))
    • functional form \(h(x)\):
      • gives different weights to different coordinates of \(x\)
      • reflects their relative importance in the credit decision
    • in this example: \(h(x)\) =linear model
      • \(H\): set of lines

Perceptron

  • Making a Decision:

    • weighted coordinates combined to form a ‘credit score’
    • resulting score compared to threshold
  • The ‘perceptron’ (using linear model)
    • \(h(x)\) = \(sign((\sum_{i=1}^dw_ix_i)-threshold)\)
    • = \(sign((\sum_{i=1}^dw_ix_i)+b)\) // b = bias
      • \(sign(s)= \begin{cases} +1, s>0\\-1, ㄴ<0\end{cases}\) (s=0 ignored for now)
      • must find decision boundary
    • \(h(x)\) = \(sign(w^Tx)\) simplified version of linear model
      • different values for parameters \(w_1, w_2, b\)
      • correspond to different lines \(w_1x_1 + w_2x_2+b=0\)
      • for simplification: treat bias \(b\) as weight \(w_0 \equiv b\)
      • introduce artificial coordinate \(x_0=1\)
      • \(w_1x_1 + w_2x_2+w_0x_0 \Rightarrow\) \(w^Tx \Rightarrow \sum_{i=0}^d w_ix_i\)
  • Roles of Learning Algorithm
    • search \(H\) by looking for weights and bias that perform well on dataset
    • produce final hypothesis \(g \in H\)

PLA

Perceptron Learning Algorithm

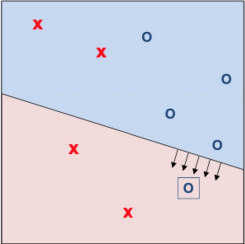
  • iterative, guaranteed to converge for linearly seperable

  • GOAL: determine optimal w based on the data to produce

  • ASSUME: data set is linearly seperable

  • Steps (continued from Perceptron)

    1. perceptron implements \(h(x) \equiv sign(w^Tx)\), given training set (x1, y1), ..., (xN, yN)
    2. PLA picks misclassified point
      • \(sign(w^Tx_n)\) \(\neq y_n\)
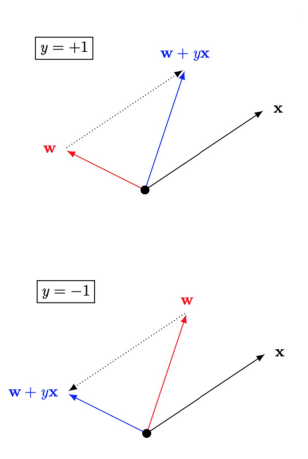
      • \(\rightarrow\) updates weight vector \(w \leftarrow w^Tx_n\) example
      • \(\Rightarrow\) rule moves boundary in the direction of classifying \(x_n\) correctly
    3. iterate until no misclassified data
      • iteration t = 1, 2, ... pick a misclassified point from (x1, y1), ..., (xN, yN) and run PLA iteration on it
      • \(w(t+1)\) \(\leftarrow w(t) + y_nx_n\) example

Example

  You want to predict if movies will be profitable based on their screenplays.
  You hire two critics A and B to read a script you have
  and rate it on a scale 1 to 4.
  The critics are not perfect. Here is the data:
  ---------------------------------------
   #  Movie Name    A     B     Profit?
  ---------------------------------------
   1  Pellet Power  1     1       -
   2  Ghosts!       3     2       +
   3  Pac is Bac    2     4       +
   4  Not a Pizza   3     4       +
   5  Endless Maze  2     3       -
  ---------------------------------------
  1. First, you want to check the linear separability of data. Plot the data on the 2D plane above, label movies with \(+\) and \(-\) and determine.
    Answer
     |    +  +
 |    -
 |       +
 |  - 
 ㅡㅡㅡㅡㅡㅡ
    • \(\Rightarrow\) Linearly Seperable
  2. Now decide to use a perceptron to classify you data. Suppose you directly use scores given above as features, together with a bias feature. That is \(f_0 = 1, f_1 =\) score given by A, \(f_2 =\) score given by B
  • Run one pass through data with perceptron algorithm, filling out the table below. Go through the data points in order (using data point #1 at step 1)
stepWeightsScoreCorrect?
1[ -1, 0, 0 ]\((-1 \cdot 1) + (0 \cdot 1) + (0 \cdot 1) = -1\)yes
2   
3   
4   
5   
Answer
- first x ($$x_0$$) = always 1 (artifical coordinate introduced)

| step |   Weights    |                       Score                       | Correct? |
| :--: | :----------: | :-----------------------------------------------: | :------: |
|  1   | [ -1, 0, 0 ] | $$(-1 \cdot 1) + (0 \cdot 1) + (0 \cdot 1) = -1$$ |   yes    |
|  2   | [ -1, 0, 0 ] | $$(-1 \cdot 1) + (0 \cdot 3) + (0 \cdot 2) = -1$$ |  ***no***  |
|  3   | <cb>[  0, 3, 2 ]</cb> | $$( 0 \cdot 1) + (3 \cdot 2) + (2 \cdot 4) = 14$$ |   yes    |
|  4   | [  0, 3, 2 ] | $$( 0 \cdot 1) + (0 \cdot 3) + (0 \cdot 4) = 17$$ |   yes    |
|  5   | [  0, 3, 2 ] | $$( 0 \cdot 1) + (0 \cdot 2) + (0 \cdot 3) = 12$$ |  ***no***  |
  • change weight when incorrect
    • after step 2: weight ([ -1, 0, 0 ] ) @ (dot product) +([ 1, 3, 2 ]) = [ 0, 3, 2 ]
    • after step 5: weight ([ 1, 3, 2 ] ) @ (dot product) -([ 1, 2, 3 ]) = [ 0, 1, -1 ]
  • \(\Rightarrow\) final weights = [-1, 1, -1]
  1. Have weights been learned that separate the data?
Answer
- $$No$$ 
- with weights `[-1, 1, -1]`, data `point 3` (−1 · 1 + 1 · 2 + −1 · 4 = −3 < 0 ) and `point 4` (−1 · 1 + 1 · 3 + −1 · 4 = −2 < 0 ) will be incorrect
  - step 2's 0 will be counted as positive
  1. Choose scenarios for which a perceptron using the features above can indeed perfectly handle a range of scenarios.
    • (a) Your reviewers are awesome: if the total of their scores is more than 8, then the movie will definitely be profitable, and otherwise it won’t be.
    • (b) Your reviewers are art critics. Your movie will be profitable if and only if each reviewer gives either a score of 2 or a score of 3
    • (c) Your reviewers are art critics. Your movie will be profitable if and only if each reviewer gives either a score of 2 or a score of 3
Answer
- (a) : can classify (considering weights `[-8, 1, 1]`)
- (b), (c): can't classify