12 Decision Trees

in Notes / Dataanalytics / Datascience

Introduction

  • non-linear Classifiers
    • non-linear decision boundary: add ‘non-linear’ features to linear model ex: logistic reg
    • use non-linear learners ex: nearest neighbors, decision trees, neural nets
    • K-Nearest Neighbor Classifier:
      • simple, often a good baseline
      • Can approximate arbitrary boundary: non-parametric
      • Disadvantage: stores all data

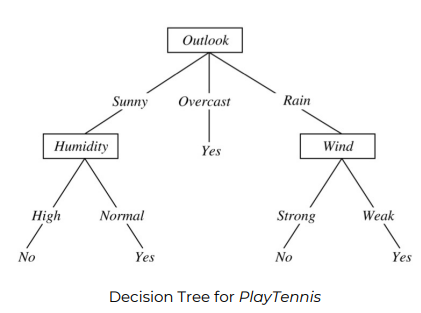
  • Decision Tree: a tree of questions that must be answered in sequence to yield predicted classification

    • nestrov
    • \(Y = (A\land B) \lor (\lnot A \land C)\) ((A and B) or (not A and C))
    • one of the most intuitive classifer, easy to understand & construct
    • 놀랍게도 굉장히 잘 된다
  • Structure of Decision Tree
    • internal nodes: attributes (features)
    • Leafs: classification outcome
    • Edges: assignment
  • Example: Logistic Regression using petal data
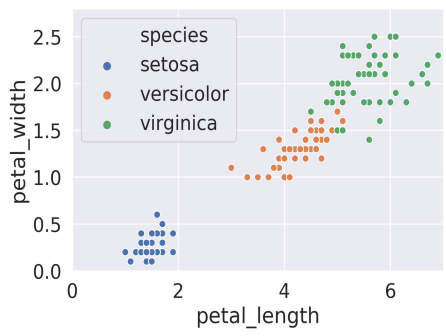
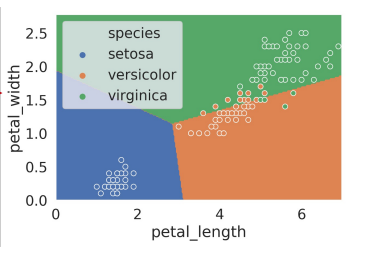
nestrov nestrov
  • logistic regression = linear \(\Rightarrow\) linear decision boundaries

Decision Tree Basics

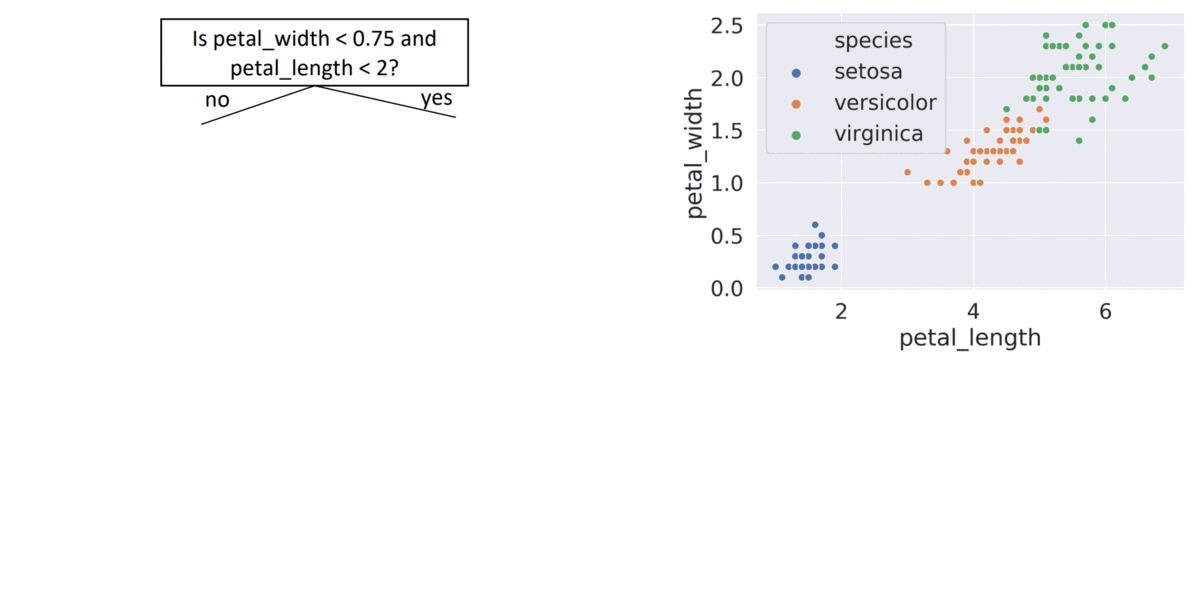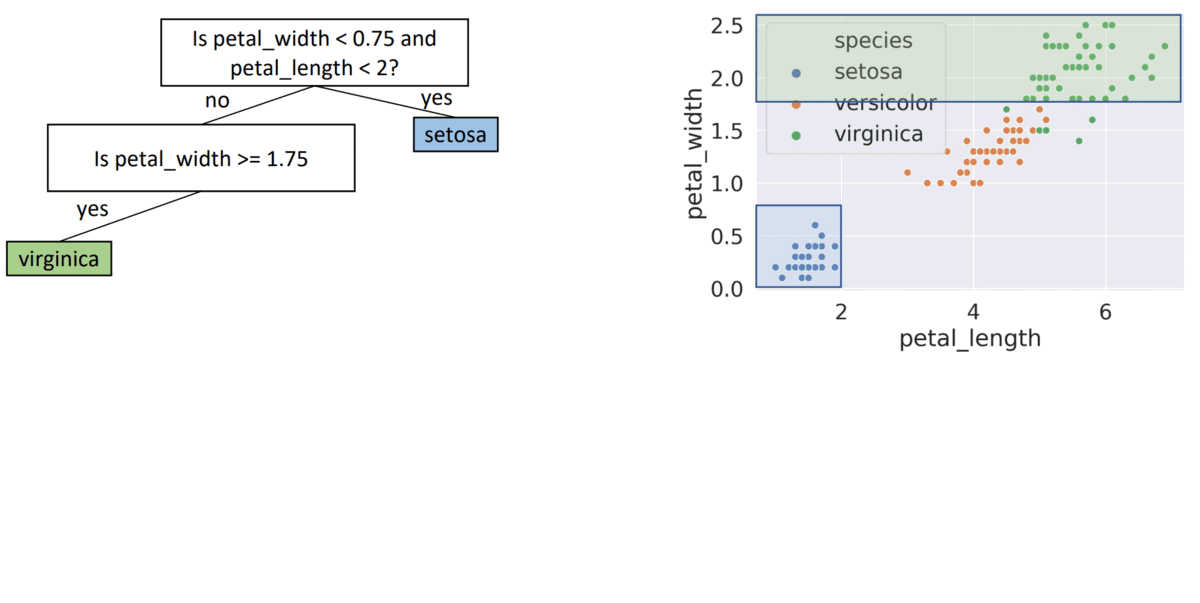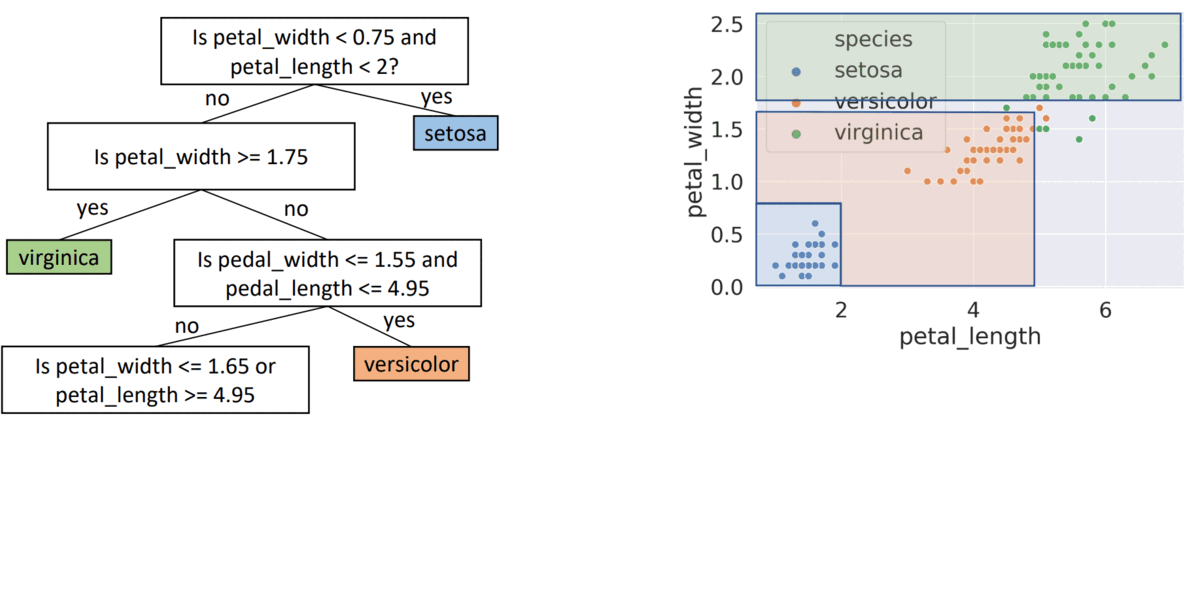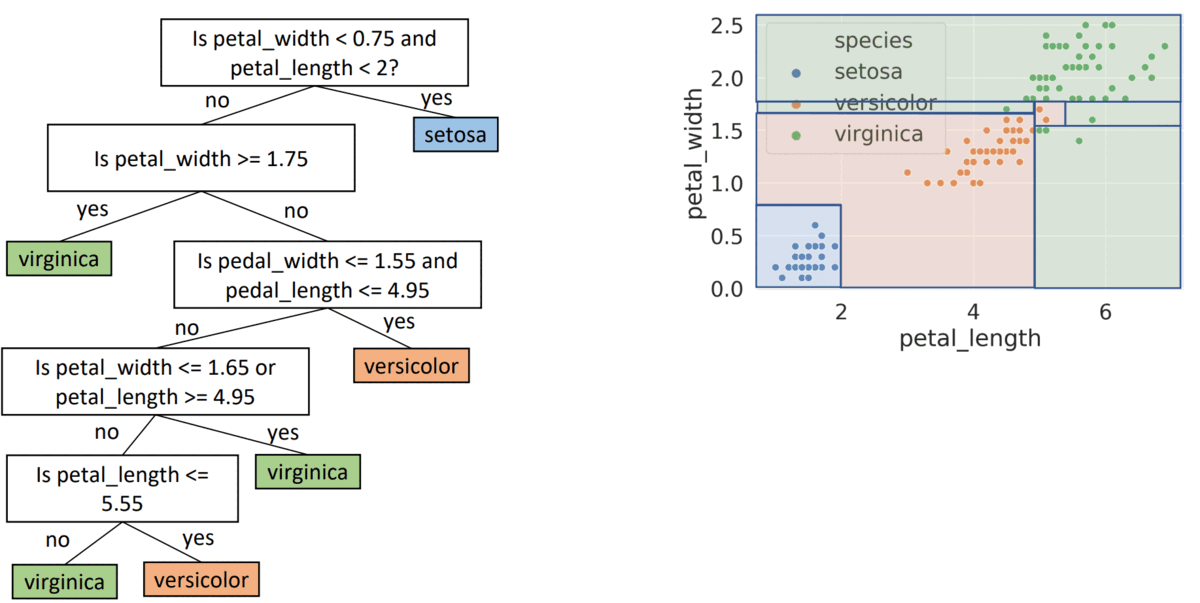
nestrov

  • seems good, gets every point correctly
  • might result in overfitting

Decision Tree Generation

Traditional Algorithm

  • all data starts in root node
  • repeat until every node is either pure(one type) or unsplittable (duplicate but not splittable)
    1. pick best feature \(x\), best split value β ( x = petal_length, β = 2 )
    2. Split Data into 2 nodes ( x < β, x >= β )
  • Learning Smallest (simplest) decision Tree : NP-complete (existing algorithms exponential)
  • Use Greedy Hueristics
    • start with empty tree \(\rightarrow\) choose next best attribute \(\rightarrow\) recurse \(\circlearrowleft\)
  • Defining Best Feature

nestrov

Node Entropy

\[node \hspace{0.1cm} entropy\hspace{0.1cm} S = -\sum _c p_c log_2p_c\]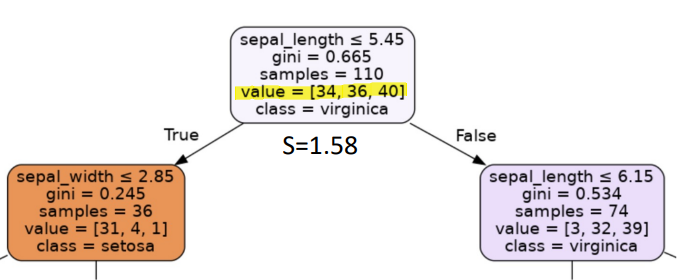

entropy

  • Entropy of Root Node
    • \(p_0=\) \(\frac{34}{110} = 0.31\)
    • \(p_1=\) \(\frac{36}{110} = 0.33\)
    • \(p_2=\) \(\frac{40}{110} = 0.36\)
    • \(S =\) \(-(0.31 log_2(0.31)) -(0.33 log_2(0.33))-(0.36 log_2(0.36))\)
    • \(S = 1.58\)
  • Entropy = 혼란도: how unpredictable a node is
    • LOW Entropy: more predictable \(\Rightarrow\) Good!
    • HIGH Entropy: more unpredictble
  • Entropy
    • 0 Entropy: data all in one class (\(-1log_2(1)=0\))
      • ex: [ 34, 0, 0 ] \(\rightarrow p_0 = \frac{34}{34} = 1\)
      • \(-1 log_2 (1) =\) \(0\)
    • 1 Entropy: data evenly split between 2 classes
      • ex: [ 4, 4 ] \(\rightarrow p_0 = \frac{4}{8} = 0.5\), \(p_1 = \frac{4}{8} = 0.5\)
      • \(-0.5 log_2 (0.5) -0.5 log_2 (0.5) =\) \(1\)
    • 1.58 Entropy: split evenly into 3 classes
      • ex: [ 4, 4, 4 ] \(\rightarrow p_0 = p_1 = p_2 = \frac{4}{12} = 0.33\)
        • \(3 \times -0.33 log_2 (0.33) =\) \(1.58\)
    • \(\Rightarrow\) data evenly split between \(C\) classes
      • \(C \cdot (\frac{1}{C}log_2(\frac{1}{C})) = -log_2(\frac{1}{C}) =\) \(log_2(C)\)
  • Weighted Entropy as a Loss Function
    • use it to decide which split to take
    • given 2 nodes (\(X, Y\)) with each \(N_1, N_2\) samples:
      • \[L=\frac{N_1S(X)+N_2S(Y)}{N_1+N_2}\]
      • \(\Longrightarrow\) MIDTERM
  • Defining Best Feature
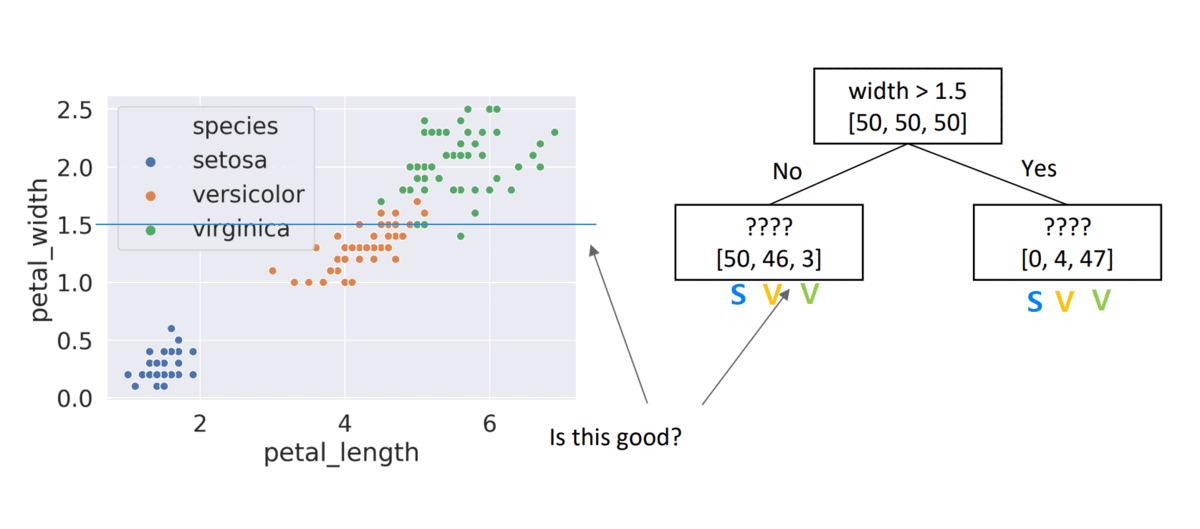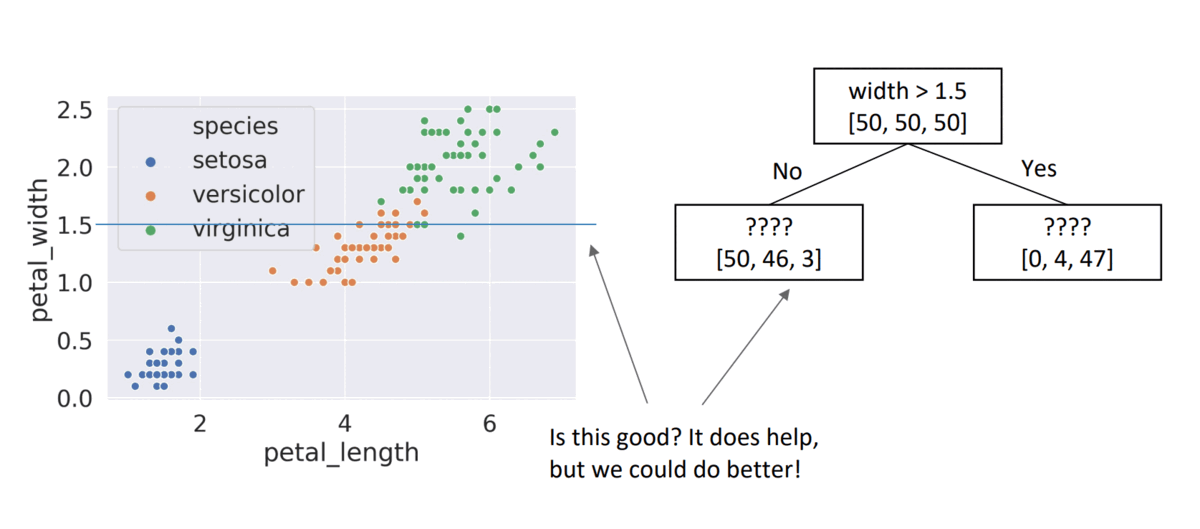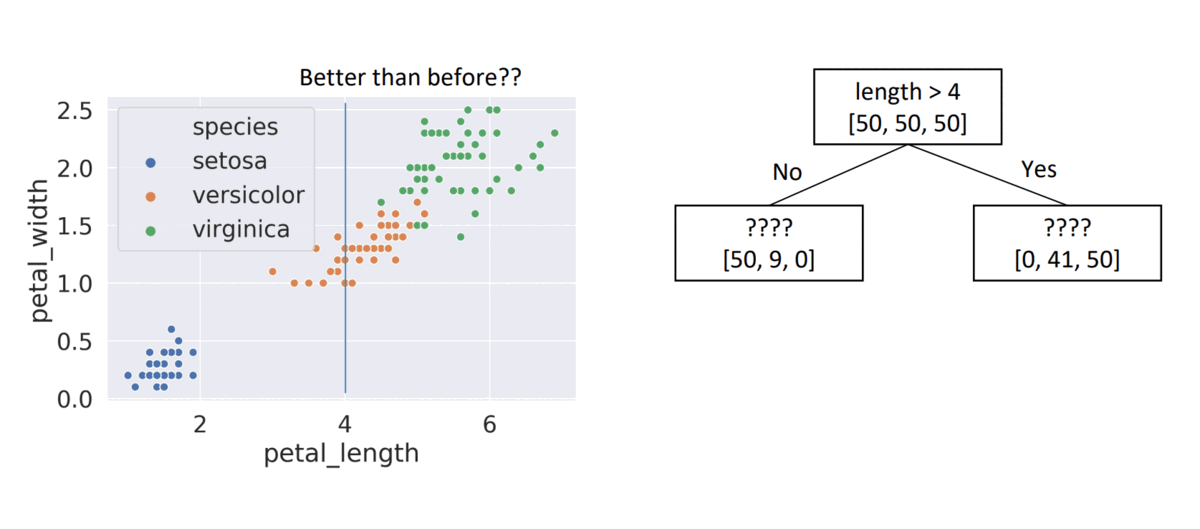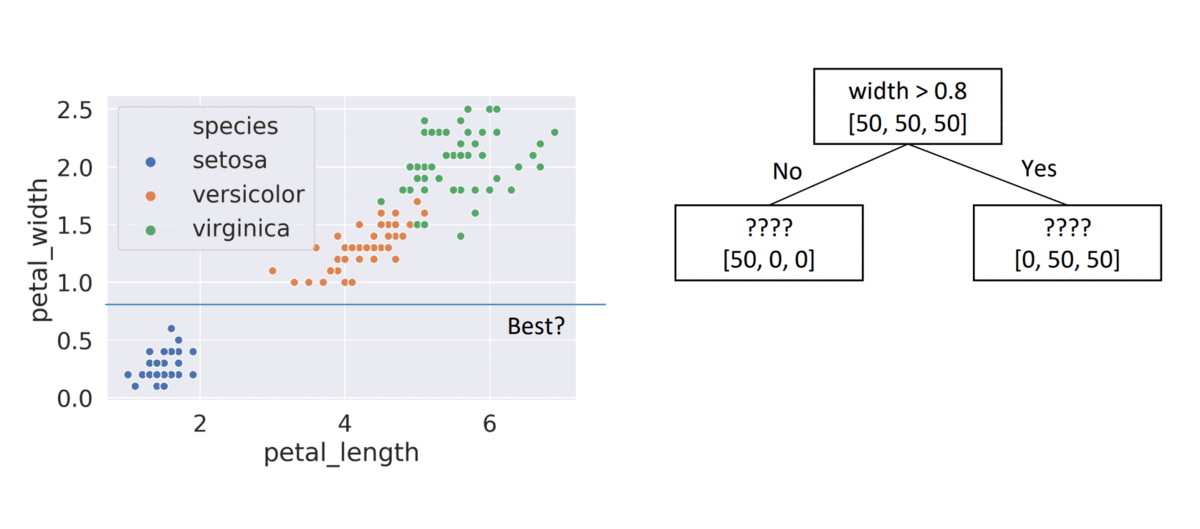
    • Choice #1: width > 1.5, child node entropies: \(entropy([50,46,2])=1.16\), \(entropy([4,47])=0.4\)
      • Weighted Average = \(\frac{99}{150}*1.16 + \frac{51}{150}*0.4 =\) \(0.9\)
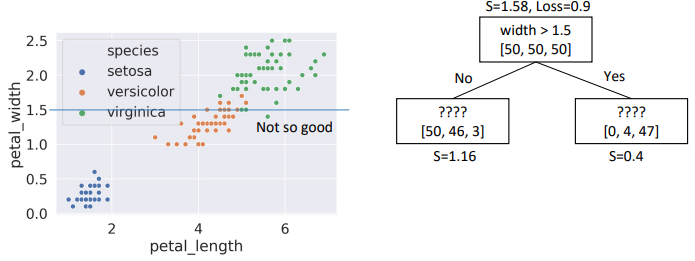
      • step1
    • Choice #2: length > 4, child node entropies: \(entropy([50,9])=0.62\), \(entropy([41,50])=0.99\)
      • Weighted Average = \(0.84\) \(\Rightarrow\) Better than choice (1)
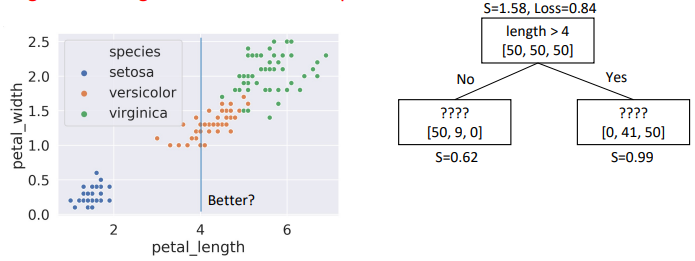
      • step1
    • Choice #3: width > 0.5, child node entropies: \(entropy([2,50,50])=1.12\), \(entropy([48])=0\)
      • Weighted Average = \(0.76\) \(\Rightarrow\) Better than choice (2)
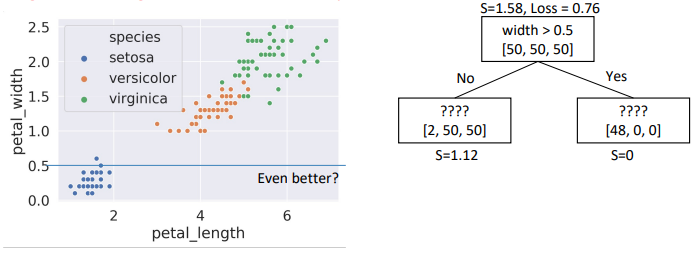
      • step1
    • Choice #4: width > 0.9, child node entropies: \(entropy([50,50])=0.1\), \(entropy([50])=0\)
      • Weighted Average = \(0.66\) \(\Rightarrow\) Better than choice (3)
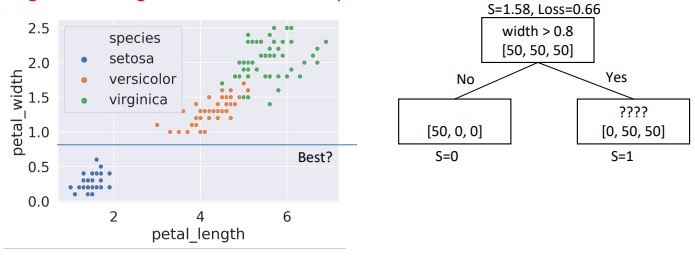
      • step1
  • \(\Rightarrow\) Traditional Decision Tree Generation Algorithm has overfitting issues

Restricting Decision Tree Complexity

  • Approaches Explained
  1. Preventing Growth: set one or more special rules to prevent growth
    • ex: don’t split nodes if <1% of sample
    • ex: don’t allow depth more than 7 levels
    • Choosing hyperparameters ?
  2. Pruning: Let trees grow fully, then cut off less usefuly branches
    • set validation set before creating tree
    • if replacing node by its most common prediction has no impact on validation error, don’t split node
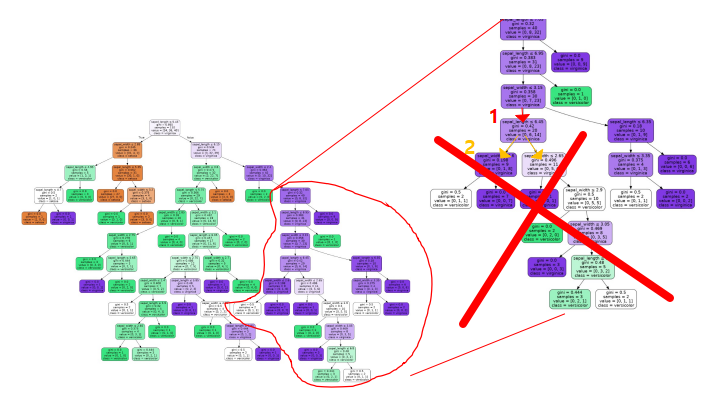
    • step1
    • if (1) and (2) does not have significan difference, prune

Random Forests

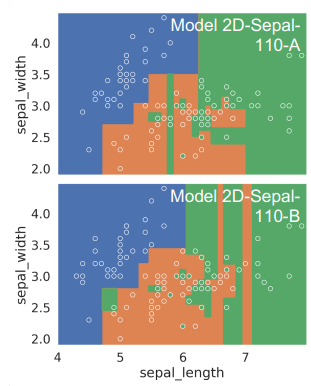
  • fully grown trees: almost always overfit data
    • low model bias, high model variance
    • \(\Rightarrow\) small changes in dataset \(\rightarrow\) very different decision tree
    Example

    step1

  • Random Forest Idea: Build many decision tress and vote

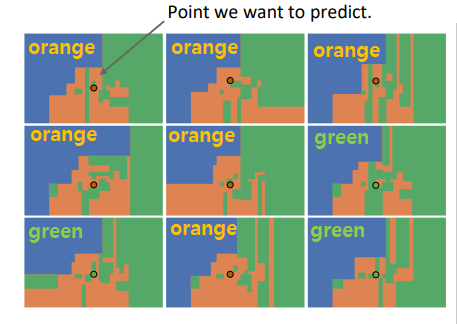
step1

  • 6 votes orange : 3 votes green \(\Rightarrow\) ORANGE

Bagging

  • Bootstrap AGGregatING

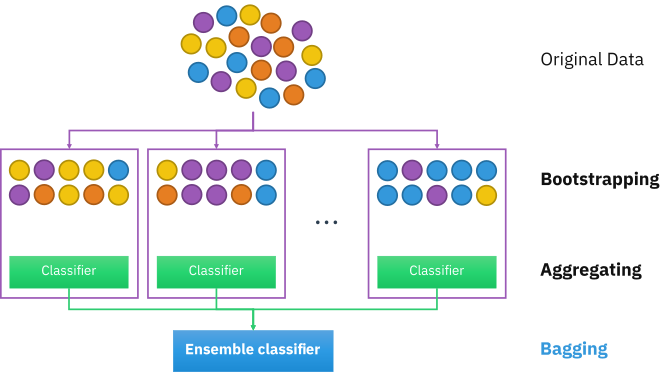
bagging

  • but bagging not enough to reduce model variance
    • decision trees look very similar to each other
    • one strong feature always used for first split
    • bagging
    • \(\Rightarrow\) only use a sample of \(m\) features at each split
      • usually \(m=\sqrt{p}\) for decision trees in classification (\(p\): # of features)

Random Forest Algorithm

  • 2 hyperparameters: T and \(m\)
1. Bootstrap training data 'T' times. Fit decision tree each resample by:
  - start with data in one node (until all nodes are pure)
  - pick impure node
  - pick random subset of 'm' features 
    → pick best feature 'x' and split value β  so that split loss is minimized 
    (ex: x = petal_width, β = 0.8 => L=0.66)
  - split data into 2 nodes (x < β, x ≥ β)
2. [predict] ask T decision trees for prediction and take majority vote
  • preventing growth, pruning, random forest \(\Rightarrow heuristics\)
    • not provably best/mathematically optimal
    • 그저 sounded good, implemented, worked well
  • Why we use Random Forests
    1. Versatile (regression & classification 가능)
    2. Invariant to feature scaling and translation
    3. Automatic feature selection
    4. nonlinear decision boundaries without complicated feature engineering
    5. 다른 nonlinear model보다 overfit 심하진 않음
    6. Example of ensemble method: combine knowledge of many simple models to create sophisticated model
    7. Example of bootstrap: reduce model variance
  • Provide alternate non-linear framework for classification & regression
    1. overfitting probability high
    2. boundaries can be more complex
    3. underlying principle fundamentally different