Interpolation, PCA/LDA, Overfitting
in Notes / Artificialintelligence / Introductiontoai
DAY 10
Interpolation vs. Linear Regression
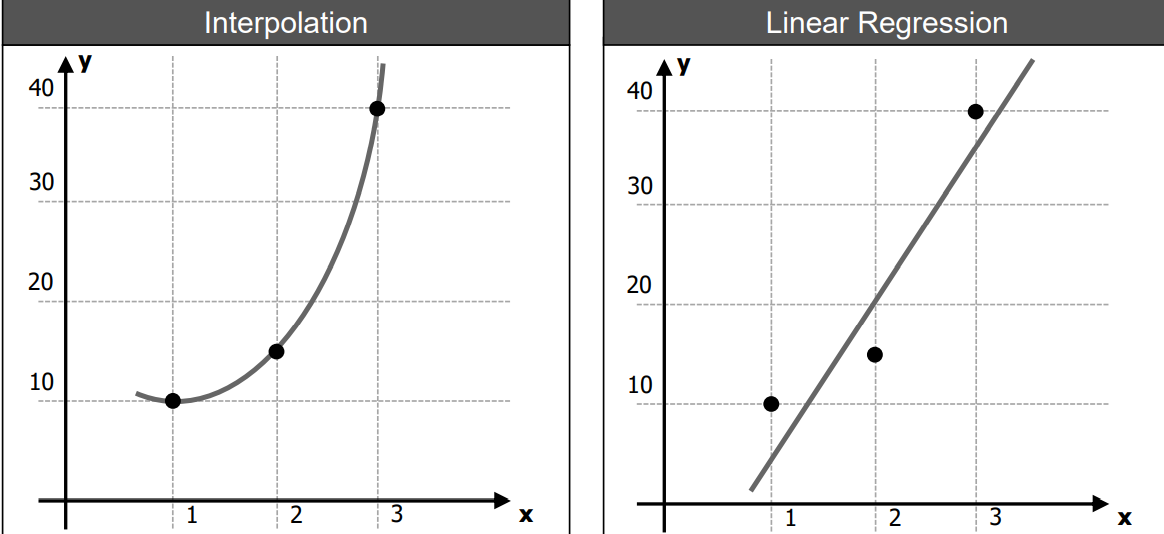
- curve does not need to be linear; goes through all points (보간법)
- Interpolation with Polynomials : \(y = x^2 +a_1 x^1 + a_0\)
FIND COEFFECIENTS \(a_2, a_1, a_0\) by putting in \((1,10), (2,15), (3,40)\)
- How is it related to Neural Network Training?
- Mathematical Meaning of Neural Network Handling
REVIEW PIC
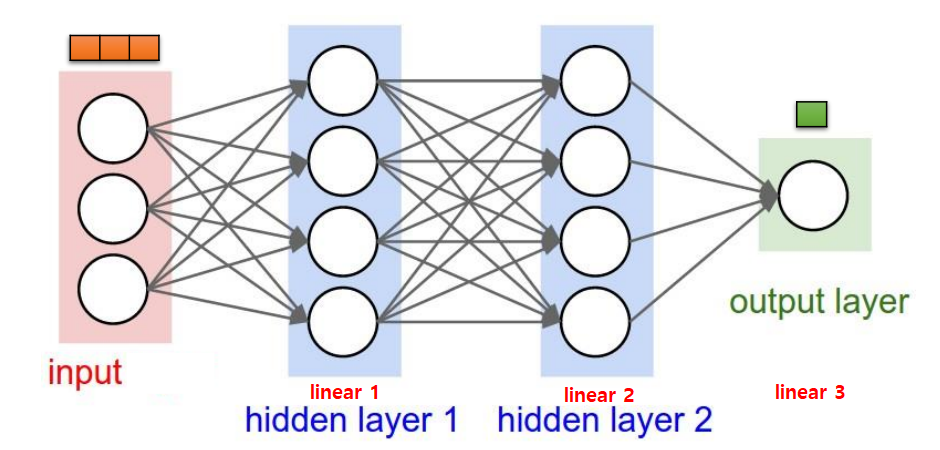
- where training data/labels are given (A LOT)
- Most well-known function approximation with neural network : Deep Reinforcement Learning
PCA / LDA
- Example : Suppose you have ( 1 x 100 ) vector, and need to choose 20 out of it
- FEATURE SELECTION : choose best 20 that fits certain criteria
- FEATURE EXTRACTION : NO CRITERIA, gotta choose \(W\) vector ( 100 x 20 ) that will make ( 1 x 20 ) vector
- HOW TO DETERMINE \(W\) Vector ? => PCA / LDA
PCA
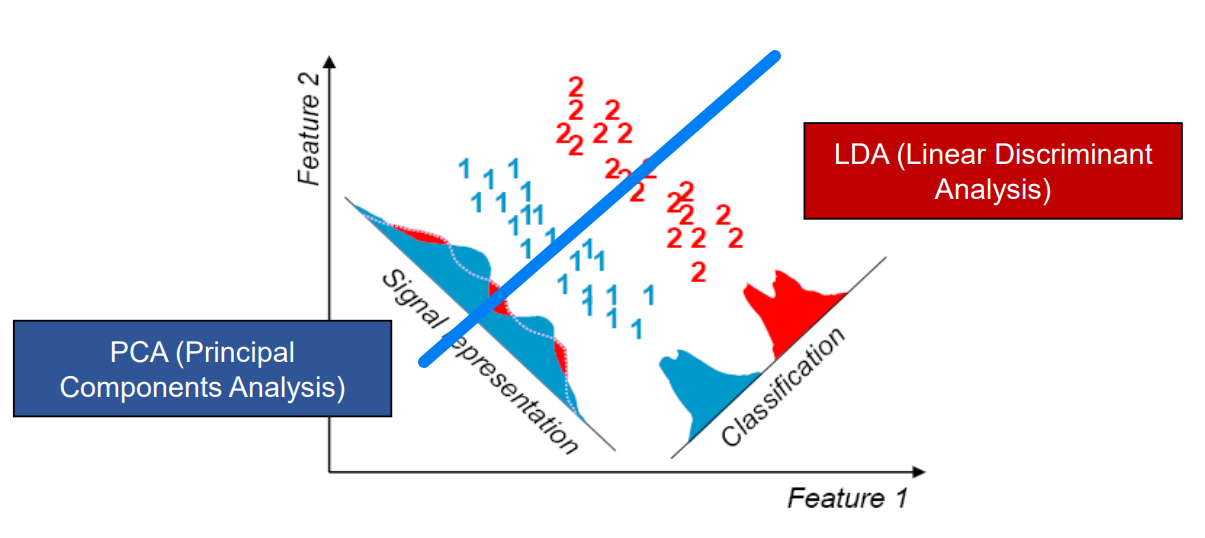
Maintains Shape - 분포의 모형을 고르기 (최대한 넓게, 겹쳐도 상관 X)
- example: Face Recognition
- color not required -> reduce dimension 3 times (eliminate RGB)
- consider only features of the face
LDA
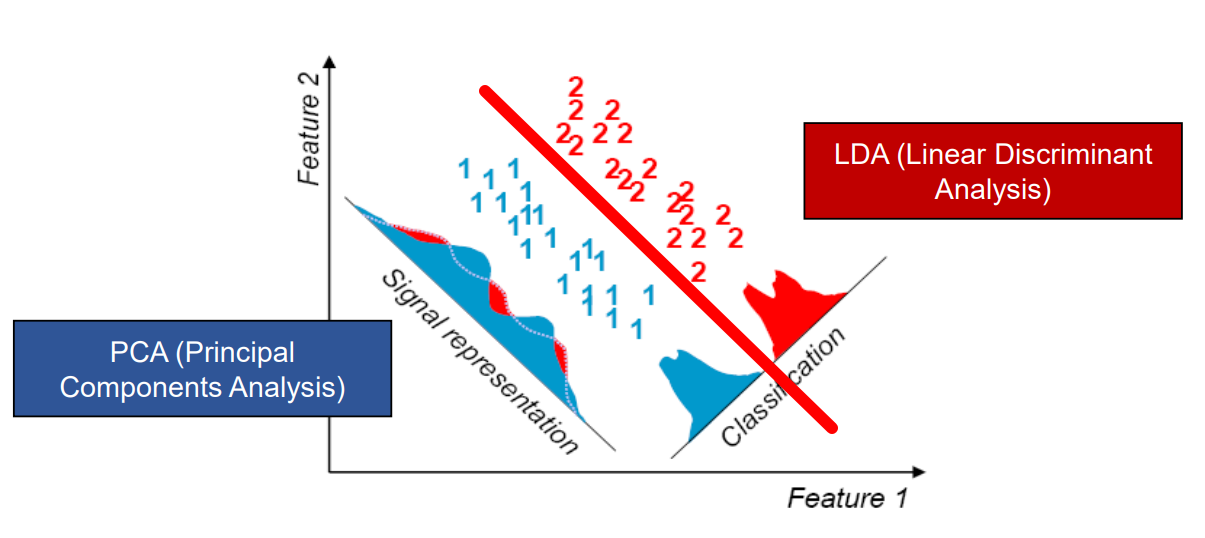
Consider Classification - Shape 고려 X, 최대한 안 섞이게 분류만 신경씀
Fisher’s linear discriminant function
\(J(w) = \frac {| \tilde \mu_1 -\tilde \mu_2 |^2 \rightarrow Maximize!}{\tilde S_1^2 -\tilde S_2^2 \rightarrow Minimize!}\)
- numerator (평균간의 거리) maximize => better classification
denominator (분산 + 분산) minimize => number gets bigger
Overfitting
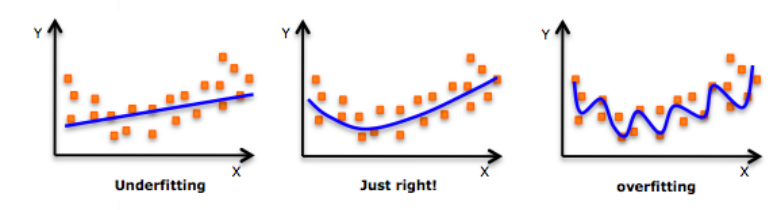
- consider the best line (model) out of three
- \(Q.\): Green Line or Black Line ?
- \(A.\): depends on how much dataset is provided
- Currently : GREEN
- Later on after more data, If TOO OVERFITTING: Smooth-ify the model (from Green to Black)
- \(A.\): depends on how much dataset is provided
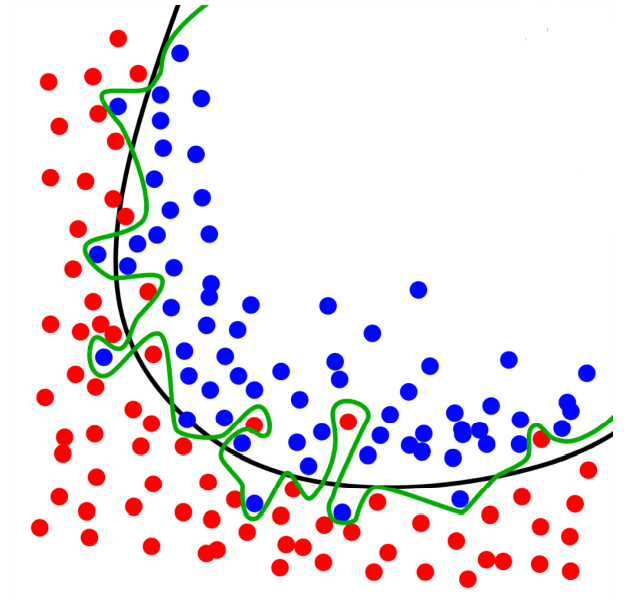
- Overfitting Problem Solutions:
- Autoencoding
- Dropout
- Regularization (생략)
Autoencoding
PCA (차원축소)
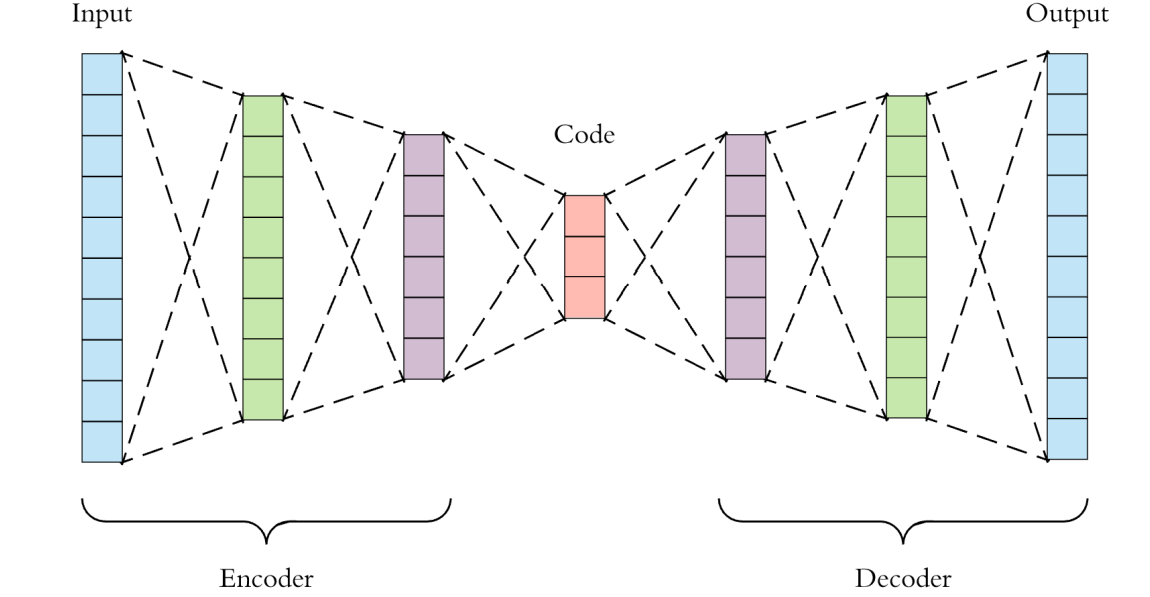
- Make the model smoother by reducing dimensions
- In Encoding Stage, outliers (필요없는, 너무 민감한 데이터) get eliminated
- In Decoding Stage, the model is enlarged to its original size (but with more smooth data)
Dropout
- easier to implement than autoencoding (popular for SW Developers)
- Autoencoding more widely used in Statistics and Theory
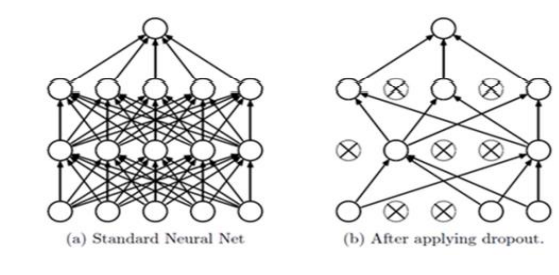
tf.nn.dropout(layer, keep_prob=0.9)
10%eliminated,90%maintained from weight values.- avoids 과한 학습
